Скажите как сделать и как всё рассписать
Другие вопросы по теме Геометрия
Популярные вопросы
- 300×50 решите в оптимальном виде...
2 - 5. Какие натуральные решения неравенства 655 x 672 кратны пяти?...
1 - и подпишуся и пролайкаю ответ...
3 - Числа в стандартном виде a)23450000, б ща сдохну...
2 - НА СТРАНИЦЫ ССЫЛКИРАССЫЛКИРЕЦЕНЗИРОВАНИЕВИДABBYY FineReader 12Анализ...
1 - Раставьте исторические события в хронологической последовательности...
2 - Қазақ тілі тжб 9 сынып барма ...
1 - 1 з кутів паралелограма на 40 градусів більший за інший знайти кути...
3 - Прочитать текст и ответить на вопросы. F или T...
3 - физика Первую половину пути равную 1800 м , турист шел со скоростью...
2
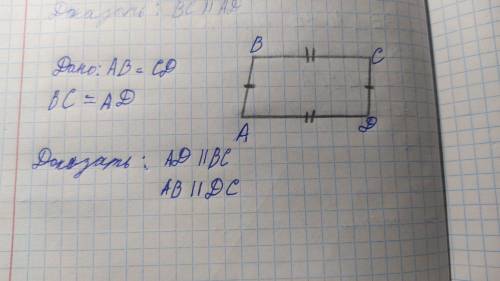
Проводим BD
1. Рассмотрим ΔABD и ΔBDC
1) BD -- общая
2) AB = CD (по усл.)
3) AD = BC (по усл.)
Следовательно, ΔABD = ΔBDC (по 3 признаку)
2. ΔABD = ΔBDC ⇒ ∠ABD = ∠BDC и ∠CBD = ∠BDA (соотв. элементы равных треугольников)
3. ∠ABD = ∠BDC -- накр. леж. при прямых AB и CD и секущей BD ⇒ AB || CD (по признаку параллельности прямых)
∠CBD = ∠BDA -- накр. леж. при прямых BC и AD и секущей BD ⇒ BC || AD (по признаку параллельности прямых)
ч. т. д.
Объяснение:
АВСД параллелограмм (противоположные стороны попарно равны: определение). В параллелограмме противоположные стороны параллельны (свойство). Следовательно АВ║СД и ВС║АД.