Синус, косинус, тангенс, котангенс. соотношения в прямоугольном треугольнике. 9 класс

Ответы

Мишa1 21.10.2020 06:24

$cos(\beta) = \frac{8}{17}.$ Найдите площадь ΔАВС.

- - -

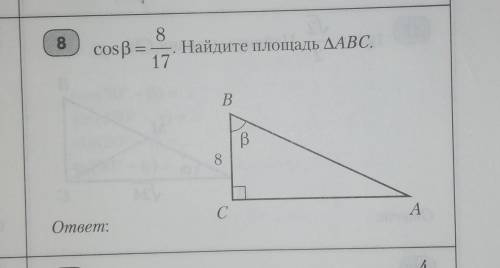
Дано :

ΔАВС - прямоугольный (∠С = 90°).

СВ = 8.

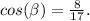
$cos(\beta) = \frac{8}{17}.$

Найти :

S(ΔABC) = ?

Решение :Косинус острого угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе.

Отсюда :

$cos(\beta) = \frac{8}{17}\\\\cos(\beta) = \frac{CB}{AB}\\\\\frac{8}{17} = \frac{8}{AB}\\\\\boxed{AB = 17}$

По теореме Пифагора :

CB² + AC² = AB²

AC² = AB² - CB² = 17² - 8² = 289 - 64 = 225

АС = √АС² = √225 = 15.

Площадь прямоугольного треугольника равна половине произведения его катетов.

Отсюда :

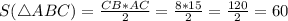$S(\triangle ABC) = \frac{CB*AC}{2} = \frac{8*15}{2} = \frac{120}{2} = 60$ (ед²).

ответ :

60 (ед²).

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

engelsvova 19.07.2019 22:20

soneta991 19.07.2019 22:20

murrtinez 04.08.2019 20:00

Lucky0ne 06.03.2020 01:25

первых задачи решить нужно...

vikaiero13 06.03.2020 01:29

Объясните данные номера по геометрии...

11041980 06.03.2020 01:29

zaira1979zaira11 06.03.2020 01:29

саня2271337 06.03.2020 01:32

Сделать вид слева в масштабе 2:1 , дам...

annatimofeeva4 02.04.2020 20:41

Розв язати 3 задачі з геометрії.Умова на фото...

ворона1111 02.04.2020 20:40

Синус, косинус, тангенс, котангенс. соотношения в прямоугольном треугольнике. 9 класс​