Sin =2/5 cos tg-? можете сказать что как делаете?

Так как значение функции sin x принимает положительные значения в первой и второй четверти, то рассмотрим два варианта:

sin²x + cos² x = 1 ⇒ cos x= √(1-sin²x)=(√21)/5 (для 0<x<90°)

cos x= -(√21)/5 (для 90°<x<180°)

tg x =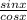 ⇒ tg x =(sin x)÷√(1-sin²x)=2/√21 (для 0<x<90°)

tg x =-2/√21 (для 90°<x<180°)

ctg x =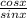 ⇒ ctg x =(√(1-sin²x))÷(sin x)=(√21)/2 (для 0<x<90°)

ctg x =-(√21)/2 (для 90°<x<180°)