Шестиугольная и треугольная правильные призмы имеют равные высоты и равные площади боковых поверхностей. разность площадей их полных поверхностей равна 4√3см.вычислить стороны их оснований
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение на тему : главный герой из повести детсво горький...
3 - Впиши вместо точек названия разрядов: 9009=9 тыс. 9 ед. 1986= 3056= 5420=...
2 - Докажите, что функция y=f (x) является возрастающей: y=x-1/x+1...
2 - Вгидравлической машине на малый поршень площадью 25 см2 действует сила...
1 - Анализ лирического произведения рубцова осенние листья. (1- тема произведения...
1 - Петя начертил 3 отрезка длина первого 4 см а каждый следующий в 2 раза...
3 - Раскройте скобки : 1) (x+5)*(x-7) 2) (x+1)*(x-3) 3)(a-m)*(m+11a) +3n)*(4n+5)...
3 - Встретились 8 леших.2 поведали о том как лучше напугать путников, 3 как...
1 - Одновременно с испарением в атмосферу вода возвращается на землю. тогда...
2 - 7предложений с вы деле нами однороднами членами по картине в.е. попков...
1
Так как площадь боковой повехности призмы вычисляется по формуле:
Так как площади боковых поверхностей равны, и равны высоты получаем равенство периметров оснований данных призм:
Площадь полной поверхности призмы численно равна сумме площадей оснований и боковой поверхности:
Так как известно что разность полных площадей равна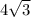 получаем:
получаем:
Получаем:
ответ: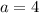 - сторона основания трехгранной призмы
- сторона основания трехгранной призмы