Сформулируйте и докажите теорему выражающую первый признак подобия треугольников

Теорема. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники являются подобными

Доказательство:

Пусть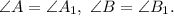 Так как сумма углов треугольника равна 180°, то для треугольников ABC и A₁B₁C₁ можем записать равенства:

Выражаем из первого равенства угол С, а из второго равенства угол C₁, получим :

, тогда , то есть у треугольников ABC и A₁B₁C₁ углы соответственно равны.

Если угол одного треугольника равен углу другого треугольника, то площади треугольников относятся как произведение сторон, заключающих равные углы.

То есть,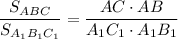 - для

Так как , то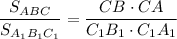

Приравнивая, получим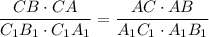 , получим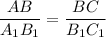

Аналогично для ∠A = ∠A₁ и ∠B = ∠B₁, имеет место равенство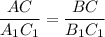

Следовательно,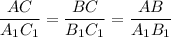 , то есть получили что стороны треугольников пропорциональны.