Сфера задана уравнением x2+(y+3)2+(z-2)2=25 a) назовите координаты центра и радиус сферы б)определите,принадлежат ли данной сфере точки а и в ,если а(4; -3; -1),в(0; 1; 3)

Уравнение сферы: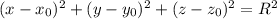 , где 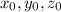- координаты центра сферы, 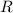- радиус сферы.

Представим уравнение, данное в задаче, в общем виде.

а) Отсюда координаты центра сферы О(0; -3; 2), радиус сферы R=5.

б) Подставим координаты точек А и В в исходное уравнение сферы. Если равенство будет выполняться, то точка принадлежит сфере.

А(4;-3;-1)

Равенство верно, значит точка А принадлежит данной сфере.

В(0;1;3)

Равенство неверно, следовательно, точка В не принадлежит данной сфере.