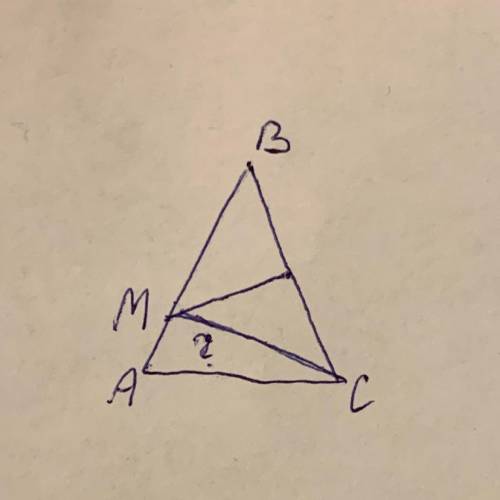
Серединный перпендикуляр боковой стороны BC равнобедренного треугольника ABC пересекает боковую сторону AB в точке M. Найдите периметр треуголника AMC, если AB=15см и AC= 7 см.

(Возможно рисунок неверный, точно не знаю)

Для начала, давайте выясним некоторые свойства равнобедренных треугольников.

Равнобедренный треугольник - это треугольник, у которого две стороны равны. В данном случае, мы знаем, что стороны AB и AC равны. Поэтому, треугольник ABC - равнобедренный.

Серединный перпендикуляр - это прямая, которая проходит через середину стороны и перпендикулярна к этой стороне. В данном случае, серединный перпендикуляр боковой стороны BC проходит через середину стороны BC и перпендикулярен к ней. Пересечение этого перпендикуляра и стороны AB обозначено точкой M.

Теперь мы можем перейти к решению задачи.

1. У нас есть равнобедренный треугольник ABC, где AB = 15 см и AC = 7 см.

2. Серединный перпендикуляр боковой стороны BC пересекает сторону AB в точке M. Обозначим длину отрезка AM как x.

3. Так как AM является серединным перпендикуляром, то BM равно MA. Также, учитывая, что треугольник ABC равнобедренный, BC равно AC.

4. Известно, что длина стороны AB равна 15 см, поэтому AM + BM = 15.

5. Теперь мы можем записать уравнение: x + x = 15.

6. Простыми математическими операциями получаем: 2x = 15, и деля обе части на 2, получаем x = 7.5 см.

7. Так как AM = x = 7.5 см, и AC = 7 см, то остается найти длину стороны MC.

8. Сумма длин сторон треугольника AMC равна периметру данного треугольника.

9. Длина стороны MC можно найти как разность сторон AC и AM: MC = AC - AM = 7 - 7.5 = -0.5 см.

10. Отрицательное значение длины стороны MC не имеет смысла в данной задаче. Вероятно, это может быть ошибка в условии или в рисунке.

Итак, мы не можем найти периметр треугольника AMC, так как нам неизвестна длина стороны MC из-за ошибки в данной задаче.