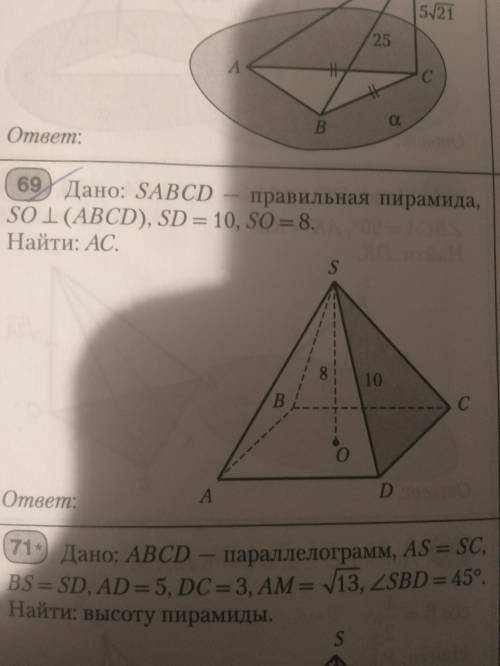
SABCD— правильная пирамида, SO⊥(ABCD), SD=10,SO=8. Найти :АС

Для решения данной задачи, мы можем использовать две теоремы:
1) Теорему Пифагора для прямоугольного треугольника
2) Теорему о высоте в прямоугольной пирамиде.

Первым шагом, мы должны определить, какие стороны заданного нам треугольника являются катетами, а какие - гипотенузой.
Поскольку треугольник AOS является прямоугольным и SO ⊥ SA, то сторона AS является гипотенузой, а SO - катетом.

Теперь, применим теорему Пифагора к треугольнику AOS:
AS² = AO² + SO²

Мы знаем, что SO = 8, поэтому можем заменить его в формуле:
AS² = AO² + 8²
AS² = AO² + 64

Теперь, нам нужно найти AO. Мы знаем, что AD = 10. Поскольку пирамида SABCD является правильной, то линия AO является высотой, и она устанавливается вниз от вершины S до основания треугольника ABCD.

Поскольку треугольник SAD также является прямоугольным, мы можем применить теорему Пифагора в этом случае:
AD² = AO² + OD²
10² = AO² + OD²
100 = AO² + OD²

Основание треугольника ABCD является равносторонним, так как пирамида ABCD является правильной. Это означает, что все его стороны равны.

Теперь нам нужно найти OD. Поскольку треугольник ACD является равнобедренным, то мы можем использовать свойство равнобедренного треугольника: основание его высоты делит его подобными сторонами напополам.

Таким образом, OD / AD = 1/2.
OD = AD / 2
OD = 10 / 2
OD = 5

Теперь можем заменить значения AO и OD в формуле для AD:
100 = AO² + 5²
100 = AO² + 25
AO² = 100 - 25
AO² = 75

Теперь, мы можем заменить значение AO в формуле для AS:
AS² = 75 + 64
AS² = 139

Чтобы найти AC, мы должны применить теорему о высоте в пирамиде SABCD:
AC² = AO² - OC²

Мы знаем значение AO², но нам надо найти OC. Однако, мы знаем, что OC и OD являются радиусами основания треугольника ABCD, и так как пирамида ABCD является правильной, все его стороны равны. Таким образом, получаем:

OC = OD
OC = 5

Теперь мы можем заменить значения в нашей формуле для AC:
AC² = 75 - 5²
AC² = 75 - 25
AC² = 50

Теперь, чтобы найти AC, мы должны извлечь квадратный корень из AC²:
AC = √50

Окончательно, получаем:
AC ≈ 7.07