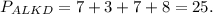SABCD - правильная пирамида, КС=5, KS=3, AD=8. Найдите Р сеч пирамиды пл.ADK
Другие вопросы по теме Геометрия
Популярные вопросы
- Почему во всех постановках пьесы на дне играет песня солнце всходит...
1 - Скорость мотоциклиста 60км/ч, а скорость страуса 1200м,мин. кто из них...
2 - Два хорошо всем известных сказочных героя загорали на палубе белоснежной...
2 - Поставити наголос у словi iрис(квiтка) iрис(цукерки)...
1 - Оксид элемента э с зарядом ядра +11 соответствует общей формуле: а)...
2 - Взяв несколько кристалликов сахара,поднесите их в пламя огня и нагрейте.сначала...
1 - Составить диалог про изучение иностранных языков)...
1 - Постройте розу ветров по следующим данным янтаря (указыается повторяемость...
2 - Используя данные современных наук согласитесь человек стал человеком...
1 - Всвоём письме роб рассказал о своей семье больше, чем миша. роб хотел...
3
25
Объяснение:
Построим искомое сечение. Так как пирамида правильная, в основании лежит правильный четырехугольник — квадрат, следовательно, Точка
Точка  лежит с прямой
лежит с прямой  в одной плоскости, поэтому сечение пройдет через точку
в одной плоскости, поэтому сечение пройдет через точку 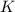 параллельно
параллельно 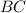 (см. рисунок):
(см. рисунок): 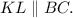 Остается соединить точки
Остается соединить точки 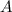 –
–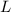 и
и 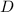 –
–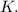
Таким образом, искомое сечение — равнобокая трапеция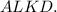
Длину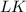 найдем из подобия треугольников
найдем из подобия треугольников 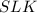 и
и 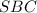 :
: 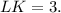
Длину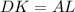 найдем, например, по теореме косинусов из треугольника
найдем, например, по теореме косинусов из треугольника 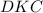 :
: 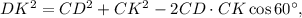
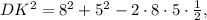
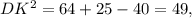
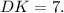
Тогда