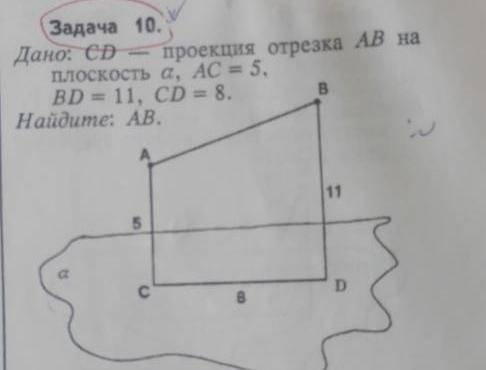
с задачей по геометрии Дано : CD - проекция отрезка AB на плоскость a, AC = 5, BD = 11, CD = 8
найти AB
Другие вопросы по теме Геометрия
Популярные вопросы
- Придумайте предложение со словом съёжился в буд.временем,во 2 лице и ёд.числе.заранее...
2 - :по рисунку 11 определите а)какая форма рельефа изображена на рисунке и что...
3 - Пространственно-временные виды искусства это подскажите...
1 - Кого из известных личностей можно назвать одиссеем и почему...
2 - Группа веществ с одинаковым типом кристаллических решеток: а) белый фосфор,...
1 - Определить объем кислорода который необходим для полного сгорания 24 л метана....
3 - Втреугольнике abc высота cd,проведённая из вершины прямого угла,делит гипотенузу...
3 - Как называется жилище в пустыне? в интернете искала, не нашла....
1 - Написать сочинение любовь, которой нет предела на основе ромео и джульетта...
2 - 3+8=15 переставьте одну спичку , так чтобы ответ был равен 15...
3
Для начала, обратим свой взгляд на треугольник ABC. Мы знаем, что CD является проекцией отрезка AB на плоскость a. Это означает, что отрезок AB является гипотенузой прямоугольного треугольника ABC.
Теперь у нас есть все необходимые значения: AC = 5, BD = 11 и CD = 8. Нам нужно найти значение AB.
Давайте рассмотрим отношения между длинами отрезков AC, BD, CD и AB. Они образуют два прямоугольных треугольника: ADC и BDC.
Используя теорему Пифагора, мы можем записать уравнения:
1. Для треугольника ADC: AC^2 = CD^2 + AD^2
Подставляем известные значения: 5^2 = 8^2 + AD^2
25 = 64 + AD^2
AD^2 = 25 - 64 = -39
AD = sqrt(-39) (извлечение корня из отрицательного числа невозможно, поэтому AD не имеет реального значения)
2. Для треугольника BDC: BD^2 = CD^2 + BC^2
Подставляем известные значения: 11^2 = 8^2 + BC^2
121 = 64 + BC^2
BC^2 = 121 - 64 = 57
BC = sqrt(57)
Теперь, заметим, что у нас уже есть отношение между длинами AB и BC. Рассмотрим треугольник ABC и вспомним, что AB является гипотенузой:
AB^2 = AC^2 + BC^2
Подставляем известные значения: AB^2 = 5^2 + sqrt(57)^2
AB^2 = 25 + 57
AB^2 = 82
Теперь мы можем найти значение AB, извлекая квадратный корень:
AB = sqrt(82)
AB ≈ 9.055
Таким образом, ответ на задачу по геометрии составляет примерно 9.055 (округлено до трех десятичных знаков).