с задачей, очень важная контрольная,

1.

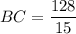
2.

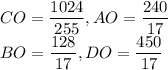
Объяснение:

1. Отложим от точки B отрезок BE такой, что он лежит на прямой, параллельной AC, а точка E лежит на прямой AD (то есть выполним параллельный перенос отрезка AC на вектор CB). Поскольку EA || BC как прямые, содержащие основания трапеции, а AC || BE по построению, то AEBC — параллелограмм, откуда BC = EA. Поскольку углы ∠AOD и ∠EBD соответственные при параллельных прямых AC и EB, то они равны, а значит, EB ⊥ BD. Но BA ⊥ ED по условию, значит, в прямоугольном ΔEBD BA — высота, опущенная из прямого угла. Тогда .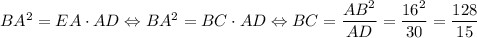

2. В прямоугольном ΔABD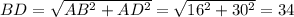 . В прямоугольном ΔABC 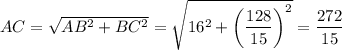. AO — высота, опущенная из прямого угла, 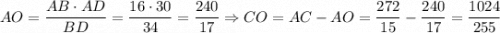. Аналогично .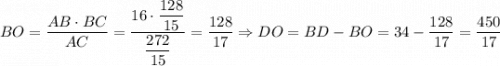