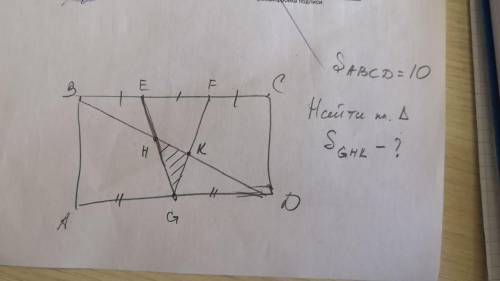
S треугольника ABC=10
Найти S закрашенной части.

Объяснение:

Прямоугольник АВСD

BE = EF = FC

AG = GD

-------------------------

-------------------------

Пусть длинные стороны прямоугольника равны а, а короткие - b.

ВС = AD = a

FD = СВ = b

Тогда площадь прямоугольника

ΔBEH ~ ΔDGH по двум углам (∠BEH = ∠DHG  - вертикальные углы; ∠HBE = ∠HDG -внутренние накрест лежащие углы при ВС║AD и секущей BD)    

Из подобия этих треугольников следует пропорциональность сторон BE = a/3 и DG = a/2, откуда , что коэффициент подобия

k = a/3 : a/2 = 2/3

Высоты этих треугольников также относятся как 2:3, и высота ΔDGH равна 3b/5. Площадь ΔDGH равна

ΔBFK ~ ΔDGK по двум углам (∠BKFH = ∠DKG  - вертикальные углы; ∠KBF = ∠KDG -внутренние накрест лежащие углы при ВС║AD и секущей BD) .    

Из подобия этих треугольников следует пропорциональность сторон BF = 2a/3 и DG = a/2, откуда  коэффициент подобия

k = 2/3 : a/2 = 4/3

Высоты этих треугольников также относятся как 4:3, и высота ΔDGK равна 3b/7. Площадь ΔDGK равна

Площадь ΔGHK