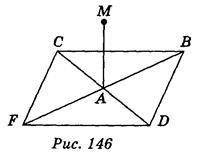
с геометрией Дан ромб CBDF, в котором АВ = 3 см, AD = 4 см, МА = 1 см. Отрезок МА перпендикулярен к плоскости АВС.

Пользуясь рисунком 146, найдите:

1) расстояние между точками М и В

2) длину отрезка MD

3) расстояние между точками А и С

4) длину отрезка BD

5) расстояние между точками М и С

6) площадь треугольника МАС

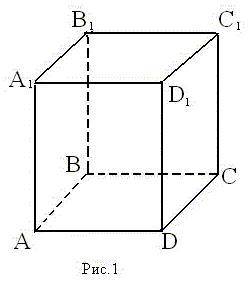
2. Дан параллелепипед (Рис 1.)

а) Назовите:

1) рёбра, перпендикулярные к плоскости (АВС)

2) плоскости, перпендикулярные ребру B1С1 б) Определите взаимное расположение:

1) прямой ВВ1 и плоскости (D1C1B1)

2) прямой A1B1 и плоскости (DCB)
3. Дано: ВМDC - прямоугольник, M ∉ (ABC), MB ⊥ AB. Доказать: CD ⊥ (ABC)

1) Расстояние между точками М и В:
Из ромба CBDF известно, что диагонали ромба перпендикулярны и делятся пополам. Поэтому MO = MB. Значит, расстояние между точками М и В равно 2 см.

2) Длина отрезка MD:
Зная, что AD = 4 см и MA = 1 см, мы можем использовать теорему Пифагора в прямоугольном треугольнике MAD.

(AD)^2 = (AM)^2 + (MD)^2
(4)^2 = (1)^2 + (MD)^2
16 = 1 + (MD)^2
(MD)^2 = 15
MD = √15 см

3) Расстояние между точками А и С:
Поскольку АВ - диагональ ромба, то АВ - это высота треугольника ASD. Поэтому расстояние между точками А и С равно 3 см.

4) Длина отрезка BD:
Из ромба CBDF мы знаем, что диагонали ромба перпендикулярны и делятся пополам. Поэтому BD = 2 * MO, где MO равно половине диагонали АС ромба CBDF.

По теореме Пифагора в прямоугольном треугольнике АОС:

(AC)^2 = (AS)^2 + (SO)^2
(3)^2 = (1)^2 + (SO)^2
9 = 1 + (SO)^2
(SO)^2 = 8
SO = √8 см

MO = SO/2 = √8/2 = √2 см
BD = 2 * MO = 2 * √2 см

5) Расстояние между точками М и С:
Расстояние между точками М и С равно длине диагонали ромба CBDF. Из ромба CBDF мы знаем, что диагонали ромба перпендикулярны и делятся пополам.

MC = 2 * MO = 2 * √2 см

6) Площадь треугольника МАС:
Площадь треугольника МАС можно найти, зная длины сторон треугольника. Мы уже нашли, что MA = 1 см и AC = 3 см. Также мы знаем, что треугольник прямоугольный, поскольку MA перпендикулярен к плоскости АВС, поэтому площадь треугольника будет равна половине произведения катетов.

Площадь треугольника МАС = (1/2) * MA * AC = (1/2) * 1 см * 3 см = 1.5 см²

2. Рёбра, перпендикулярные к плоскости (АВС):
В параллелепипеде ABCD1D2C2C1B1B ребра, перпендикулярные к плоскости (АВС), это ребра AA1, BB1 и CC1.

Плоскости, перпендикулярные ребру B1C1:
Плоскости B1C1D1 и B1C1D2 перпендикулярны ребру B1C1.

Взаимное расположение прямой ВВ1 и плоскости (D1C1B1):
Прямая ВВ1 лежит в плоскости (D1C1B1), поэтому они пересекаются.

Взаимное расположение прямой A1B1 и плоскости (DCB):
Прямая A1B1 не лежит в плоскости (DCB), она пересекает ее.

3. Доказательство CD ⊥ (ABC):
Из данного условия видно, что прямоугольник ВМDC не содержит вершину А. Поэтому при доказательстве CD ⊥ (ABC) мы можем использовать свойства параллелограмма.

Поскольку BM ⊥ AB, а ВМDC - прямоугольник, то по свойству параллелограмма диагонали параллелограмма взаимно перпендикулярны.

Таким образом, CD ⊥ (ABC).