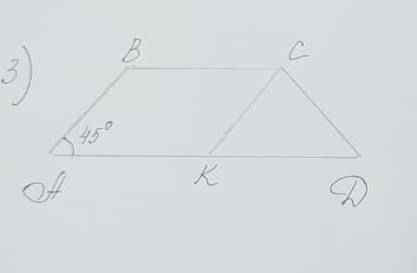
С ГЕОМЕТРИЕЙ ABCD равнобокая трапеция, ABCK параллелограмм. Угол A=45 градусов, ВС=10см, AD=14см
Найти S=ABCD, S=ABCK, S=KCD
Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите самое малое значения функции f(x) 3xв четвертом сиепени - 8...
2 - Перевести пару предложений на . не знаю что написать про жизнь студента....
2 - Уравнение реакции, отражающее превращение серы(0) в серу (-2) 1) s+cl2=scl2...
3 - Осуществить следующие превращения: hbr → kbr → br2 → cabr2...
3 - 27.139+(х-246)=29.345 решить уровнение с ответом ,проверкой ,в столбик...
1 - 8класс решить, назвать вещества и тип реакции: na-- na2o-- naoh-- zn(oh)2--...
3 - Решить ! ; миша шёл из одного села в другое 0,7 ч по полю и 0,9 ч через...
2 - Длина электромагнитной волны 10 см.найти период волны....
3 - Выражения а)(c^2)^4*c^5/c^12 б)(x+5)*(x-3)+(x-5)*(x+5) в)(3a+7)^2-42a...
1 - Ксоциально значимым признакам определяющим положение человека в обществе...
3
Объяснение:
Решение: из условия АВСК- параллелограм, => <А=<К=<С=45
=> ∆КСД-<С=90, (<А=<Д=45 по условию) КД - гипотенуза, КС=СД - катеты, КС=СД=КД*√2/2=2√2
Высота трапеции h = KД/2=2,
Трапеция-S(АВСД)=1/2*(ВС+АД)*h
S(АВСД)=1/2*(10+14)*2=24
Параллелограмм-S(АВСК)=ВС*h
S(АВСК)=10*2=20
Треугольник-S(KCD)=1/2*KD*h
S(КСД)=1/2*4*2=4
Проверка:
S(ABCD)=S(ABCK)+S(KCD)
24=20+4=24