с геометрией (9 класс)
Треугольник МКТ, сторона МК=20, М=45°, Т=60°. Найти: x и у.
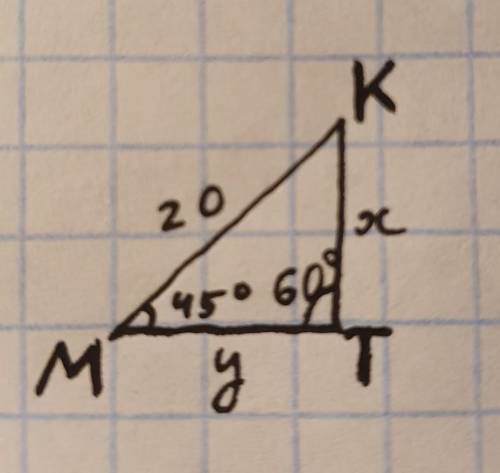
Другие вопросы по теме Геометрия
Популярные вопросы
- за ответ, неправильные буду жб....
2 - Даны длины трёх отрезков. Определи, могут ли эти отрезки быть...
2 - Звуконаслідовані слова є в реченні?...
2 - Как вы понимаете последнее предложение текста отвечая на этот...
3 - 1.вилы опыления цветов. 2.какое значение в жизни растений имеет...
3 - 2.Вставьте пропущенные прилагательные, описывающие в тексте персонифицированную...
1 - Як маленький принц доглядав за своєю планетою...
2 - 2Х8-8Х дуже треба і чим скоріше...
1 - В 100 грамм воды 20 грамм лимонной кислоты определить массовую...
1 - Верно ли ? да или нет (письменно в тетраде пишем номер задание...
1
1. Найдем сторону КТ с помощью закона синусов. В треугольнике МКТ у нас есть значение угла Т (60°), значение стороны МК (20) и значение угла М (45°). Используя формулу:
син Т / КТ = син М / МК
подставляем известные значения:
син 60° / КТ = син 45° / 20
Для решения этого уравнения сначала найдем синусы этих углов.
син 60° = √3/2
син 45° = 1/√2
Подставим значения:
√3/2 / КТ = 1/√2 / 20
Перемножим значения и упростим выражение:
√3 / КТ = 1 / (20√2)
√3 / КТ = √2 / 40
Теперь найдем КТ, выполнив обратные операции:
КТ = (√3 * 40) / √2
КТ = (40√3) / √2
КТ = (40√3) √2 / 2
КТ = (40 * √6) / 2
КТ = 20√6
Таким образом, сторона КТ равна 20√6.
2. Теперь приступим к нахождению сторон МУ и КУ. Для этого воспользуемся законом косинусов. Этот закон позволяет нам найти длину стороны треугольника, если нам известны длины двух других сторон и угол между ними.
Для стороны МУ, значение угла М равно 45°, сторона МК равно 20, а сторона КТ равна 20√6.
cos М = (МК^2 + МУ^2 - КТ^2) / (2 * МК * МУ)
Подставим значения:
cos 45° = (20^2 + МУ^2 - (20√6)^2) / (2 * 20 * МУ)
Упростим:
1 / √2 = (400 + МУ^2 - 240 * 6) / (40 * МУ)
1 / √2 = (400 + МУ^2 - 1440) / (40 * МУ)
1 / √2 = (МУ^2 - 1040) / (40 * МУ)
Умножим обе части уравнения на 40 * МУ:
40 * МУ / √2 = МУ^2 - 1040
Раскроем квадрат:
40^2 * МУ^2 / 2 = МУ^2 - 1040
1600 * МУ^2 = 2МУ^2 - 2080
Перенесем все члены уравнения на одну сторону:
0 = 2МУ^2 - 1600МУ^2 - 2080
Упростим:
0 = (2 - 1600)МУ^2 - 2080
0 = (-1598)МУ^2 - 2080
Теперь нам нужно найти значение МУ. Воспользуемся формулой дискриминанта:
D = b^2 - 4ac
где коэффициенты a, b и c в нашем случае равны:
a = -1598
b = 0
c = -2080
Подставим значения и найдем дискриминант:
D = (0)^2 - 4(-1598)(-2080)
D = 0 - 4(3187640)
D = -12750560
Так как дискриминант отрицательный, нет решений для данного уравнения. Это означает, что значение МУ является мнимым числом и решение задачи невозможно.
В результате, имея изначальные данные стороны МК, значение угла М и значение угла Т, мы смогли найти сторону КТ, которая равна 20√6. Однако, мы не смогли найти стороны МУ и КУ, так как их значения оказались мнимыми числами.
В итоге, ответ на задачу: x = 20√6, y = несуществующий (мнимый).