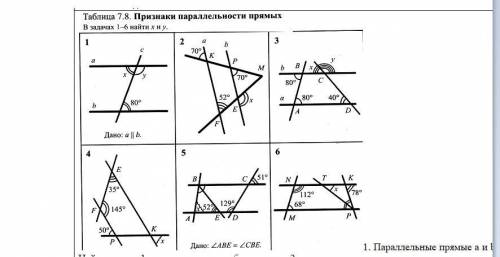
С ГЕОМЕТРИЕЙ 7 КЛАСС. Признаки параллельных прямых. В задачах 1-6 найти x и y.

Добрый день! Благодарим вас за вопрос о геометрии. Для решения задач на параллельные прямые, нам необходимо рассмотреть признаки параллельности прямых.

Признаки параллельности прямых:
1. Углы, образованные параллельными прямыми и пересекающей их прямой, равны между собой. Этот признак используется в задачах 1 и 2.
2. Кстати, в задачах 5 и 6 нам также понадобится признак перпендикулярности прямых: две прямые перпендикулярны друг другу, если углы, которые они образуют с пересекающей их прямой, являются смежными и равными.

Теперь передадимся к решению задач.

Задача 1: Найдем значения x и y.
MK || DE

Для начала заметим, что угол EFD и угол GKM находятся между параллельными прямыми и пересекающей их прямой. По признаку 1 они равны между собой.
Угол EFD = 70°

Также заметим, что угол GKM и угол LKM являются вертикальными (они находятся между параллельными прямыми). Так как угол GKM равен 70°, то и угол LKM также равен 70°.

Теперь обратим внимание на треугольник LKN. Углы LKN и LNK образуют прямой угол, так как прямая горизонтальна. По признаку 2, они являются перпендикулярными и, следовательно, равными.
Угол LKN = 90°

Таким образом, мы можем решить уравнение:
70° + 70° + x = 180°
140° + x = 180°
x = 40°

Так как угол EKP - это угол LKP, который также равен 40°, то y = 40°.

Ответ: x = 40°, y = 40°

Задача 2: Найдем значения x и y.
EA || GD

Перейдем к анализу углов. Заметим, что угол BEC и угол HEG находятся между параллельными прямыми и пересекающей их прямой. Исходя из признака 1, эти углы должны быть равны между собой.
Угол BEC = 70°

Вернемся к треугольнику HDE. Углы HDE и DHE образуют вместе прямой угол. По признаку 2, они являются перпендикулярными, а значит, равными между собой.
Угол HDE = 90°

Теперь мы можем составить уравнение:
x + 70° + 90° = 180°
x + 160° = 180°
x = 20°

Так как угол DEH - это угол DEG, который равен 20°, то y = 20°.

Ответ: x = 20°, y = 20°

Я надеюсь, что ясно объяснил решение задач. Если у вас еще остались вопросы, не стесняйтесь и задавайте их!