с геометрией 3 задачи очень , заранее благодарю . 1.Найдите площадь треугольника , если стороны АВ=8м ; ВС=7м; sin β (Бетта)=5/7 .

2.Стороны треугольника равны АВ=4м; АС=5м ;ВС=5м . Найти sin α(альфа).

3.Площадь треугольника равна 8 см ^2 (в квадрате ) . Найти сторону АС , если сторона ВС=5см ; cos ∠С=3/5.

∠-угол
/-дробная черта

1.

Зная 2 стороны и угол между ними, мы можем найти третью сторону — по теореме косинусов.

Косинус бетты мы найдём по её синусу:

β = 45°.

Теперь, чтобы найти третью сторону — используем теорему косинусов:

Теперь, зная все стороны треугольника, найдём площадь — по теореме Герона:

Вывод: S = 20.56.

2.

Для вычисления синуса альфы, нам потребуется знать косинус альфы, а для вычисления этого же косинуса, нам и сторон достаточно — используем теорему косинусов:

Этим следует:

Вывод: sinα = 0.92.

3.

Найдём синус гаммы:

Формула вычисления площади, через 2 стороны и синус — такова: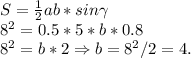

Вывод: AC = 4.