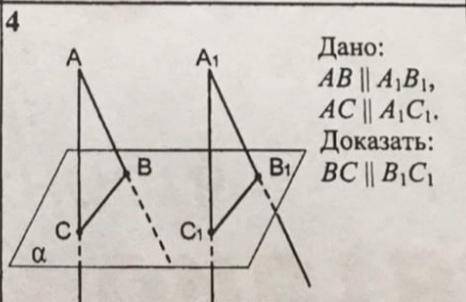
с доказательством, геометрия 10 класс. ab||a1b1, ac||a1c1. доказать bc||b1c1

Для доказательства того, что bc||b1c1, нам необходимо использовать основные теоремы о параллельных прямых и их свойствах.

Из условия задачи мы знаем, что ab||a1b1 и ac||a1c1.

Теперь давайте рассмотрим углы, образованные этими прямыми.

1. Углы a и a1: a и a1 являются соответственными углами между параллельными прямыми ab и a1b1. По теореме о соответственных углах мы знаем, что эти углы равны.

2. Углы b и b1: b и b1 являются внутренними друг относительно параллельных прямых ab и a1b1. Исходя из теоремы о внутренних углах между параллельными прямыми, эти углы также равны.

Теперь давайте рассмотрим треугольники abc и a1b1c1.

3. Треугольник abc: в этом треугольнике мы знаем, что углы a и b равны (из пункта 1), поскольку они являются внутренними углами параллельных прямых ab и ac. Исходя из свойства треугольников, угол c будет равен 180° - (а + b). Таким образом, у нас есть угол c с заданным значением.

4. Треугольник a1b1c1: в этом треугольнике у нас есть углы a1 и b1, которые, как мы уже обсуждали, равны. Но у нас также есть угол c1, о котором мы ничего не знаем.

Если мы сможем доказать, что угол c1 равен углу c, то это будет означать, что прямые bc и b1c1 параллельны.

5. Докажем, что угол c1 и угол c равны:
a) Рассмотрим параллельные прямые ac и a1c1. Из этого следует, что угол ac1 будет равен 180° - a1 (так как угол ac1 и угол a1 равны, так как они соответственные углы).
b) Также, из параллельных прямых ab и a1b1, следует, что угол ab1 равен 180° - a1 (так как угол ab1 и угол a1 являются соответственными углами).
c) Теперь рассмотрим треугольники ab1c и ac1c1. В обоих треугольниках у нас есть два угла с одинаковыми значениями: 180° - a1 и b. Следовательно, третьи углы должны быть равны, то есть угол c равен углу c1.

Из пункта 5 следует, что угол c1 и угол c равны. Из теоремы о параллельных прямых следует, что прямые bc и b1c1 параллельны.

Таким образом, было доказано, что bc||b1c1.