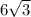С, 50 к плоскости α проведена наклонная ab (a∈α). длина наклонной равна 12 см, наклонная с плоскостью образует угол 60°. вычисли, на каком расстоянии от плоскости находится точка b. расстояние от точки b до плоскости равно −−−−−√ см (если в ответе нет корня, то под корнем пиши 1)
Другие вопросы по теме Геометрия
Популярные вопросы
- Обчисліть масову частку лугу в розчині масою 60 г, в якому розчинено...
3 - Раствор содержит соль и воду соль составляет 12% раствора сколько...
1 - Уменьшим 48 на 8 , скоко будет?...
3 - Какие мероприятия проводились для экономического восстанов-ления...
3 - Определение магнитного поляЦель: выяснить, на каком расстоянии...
2 - Арифметикалық орта :мысал жазындаршы өтінем ...
1 - Які характерні риси рослинності екваторіальних широт...
1 - СОР! Төменде берілгендердің қайсысы гиперсілтеме қойған жағдайда...
3 - Помагите 4 класс как зделоти...
1 - Как правильно пишется слово палисадник?...
2
Проведем от точки В к плоскости α перпендикуляр ( назовем эту точку О)
у нас получился прямоугольный треугольник АВ с гипотенузой АВ=12 и углом =60°
мы можем найти угол АВО = 90-60=30°(по св. прям. тр.)
По другому свойству мы можем найти АО( катет, напротив которого угол в 30°)
АО равняется половине гипотенузе, а значит 6 см
По теореме Пифагора находим расстояние от точки В до плоскости (или ВО):
ВО²=АВ²-АО²
ВО²=144-36=108
ВО=
ответ: