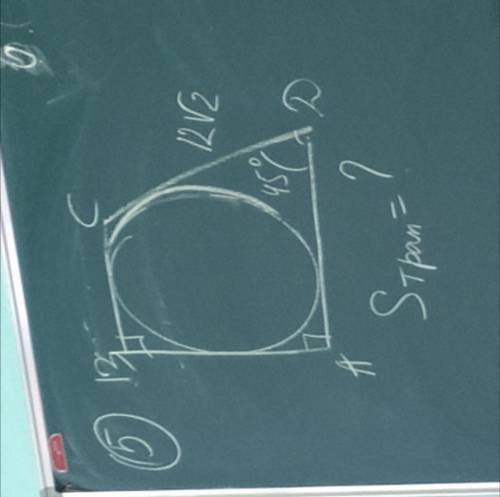
Другие вопросы по теме Геометрия
ske4
28.03.2020 12:12
dadshka
28.03.2020 12:17
pravikvdushe
28.03.2020 12:11
Ksyufenka
28.03.2020 12:11
miì02
28.03.2020 12:15
nikitakyznecov703
26.04.2019 17:32
этофиаскобратан4
26.04.2019 19:15
alena667
26.04.2019 19:11
bezhkinyova
26.04.2019 19:11
Популярные вопросы
- Найдите пропущенное число: 6 )\ +3,015=3,605 ; 10)(18,325+10,7)-\ =0,375 ....
1 - Дано треугольник ABC. B 153 градуса ,в треугольнике проведени висоти АМ и СN...
3 - можете написать ответы умоляю...
2 - Розділові знаки у СБР. Установіть відповідність:...
2 - В треугольнике MNK MNK из вершины NN проведена высота NS NS так, что...
1 - В предложение подчеркнуть прилогательные: У него голова узкая,красивая, а на...
3 - Boint 5 incas come so wenig...
3 - 1. Какая мерка определяет ширину юбки? 2. По какой мерки ( формула) рассчитывается...
3 - Какие особенности характерны для речи старушки из рассказа «Старый гений»?...
1 - Закончи предложение Насмешливо указать на определенные недостатки человека...
2
1) СК⊥AD
2) Р/м ΔСКD, ∠К=90°, ∠D=∠C=45°, значит СК=КD=х
3) BA=CK=12 - высота (т.к противоположные стороны описанного четырёхугольника равны между собой)
4) ВС+AD=12+12√2
5) Sabcd=(BC+AD)*BA/2=(12+12√2)*12/2=6*(12+12√2)=6*12(1+√2)=72(1+√2)
ответ: 72(1+√2)