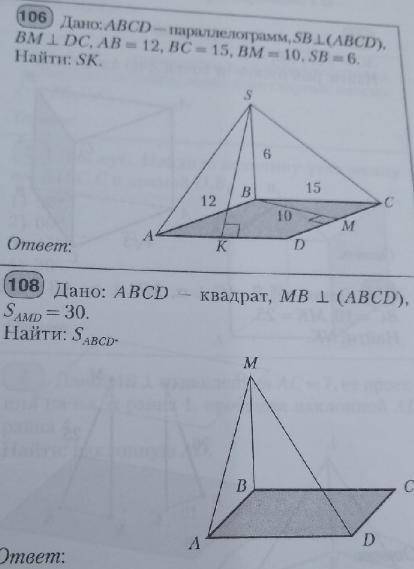
Решите задачу по геометрии и если сможете то ещё и 108
Другие вопросы по теме Геометрия
Популярные вопросы
- 640:8+480:3-23×4 по действиям...
3 - Социологические службы города Z провели опрос 40-летних работающих...
3 - Вставь пропущенные слова в рассказ Микаэлы о своих родствениках...
1 - решить 3 билета...мне очень очень это нужно...я не могу решить...
2 - . 238. Подберите синонимы по образцу: 1,5 - один с половиной,...
3 - Отзыв о военном фильме или песни , отношение к 9 маю и будет ли...
3 - Уравнениещелочной гидролиз + этилформиат...
2 - природные зоны зарубежной европы...
1 - Решение системы линейных уравнений с двумя переменными сложения...
2 - Знайдіть три послідовних цілих числа, якщо потроєний квадрат меншого...
2
Для решения этой задачи мы можем использовать свойство серединного перпендикуляра. Оно гласит, что серединный перпендикуляр к отрезку есть его высота, а также является его медианой и медиатрисой.
Из этого свойства следует, что отрезок EF является высотой треугольника CED и медианой треугольника CDF.
Для начала, найдем длину отрезка EF. Заметим, что отрезок EF параллелен отрезку CD, так как они оба перпендикулярны отрезку AB. Также мы знаем, что точка E является серединой отрезка CD. Значит, отрезок EF также является половиной отрезка CD.
Теперь обратимся к длине отрезка CD. Здесь нам может помочь теорема Пифагора, так как мы имеем дело с прямоугольным треугольником CED. По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы. Так как отрезки DC и CE перпендикулярны и образуют прямой угол, то можно записать уравнение: DC^2 = EC^2 + DE^2. Мы знаем, что точка E — середина отрезка CD, поэтому CD = 2 * EC. Подстановка этого значения даст нам: (2 * EC)^2 = EC^2 + DE^2. Преобразуя это уравнение, получим: 4 * EC^2 = EC^2 + DE^2. Вынесем EC^2 за скобки: 3 * EC^2 = DE^2.
Теперь мы можем найти отношение длины EF к длине CD. Мы знаем, что EF = 0.5 * CD и что EC^2 = (1/3) * DE^2. Подставим значения: EF = 0.5 * CD = 0.5 * (2 * EC) = EC, так как 2 * EC = CD, и DE^2 = 3 * EC^2.
Теперь у нас есть выражение для отношения EF к CD: EF/CD = EC/EC = 1. Значит, отношение длины EF к длине CD равно 1.
Таким образом, мы получаем, что EF и CD имеют одинаковую длину и отношение их длин равно 1.
Я надеюсь, что объяснение было понятным и правильным. Пожалуйста, дайте знать, если возникнут дополнительные вопросы.
Ответ на задачу 108:
К сожалению, на предоставленной картинке нет информации, необходимой для решения задачи, связанной с числом 108. Поэтому я не могу решить эту задачу без дополнительных данных. Будьте добры предоставить недостающую информацию или уточнить условие задачи, чтобы я мог её решить.