Решите задачу по Геометрии
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. Почему национальная интеллигенция с удовлетворением встретила известие...
3 - Определите, какая тригонометрическая функция угла K выражается дробью...
1 - Чи всі тварини входять до ланцюга живлення?...
2 - Опишите, что скрипт сделает для Sprite 1, если условие выполнено....
3 - Запишите пять деяний императора Нерона. Оцените одно из них, как вы...
2 - Complete the sentences with the words in the box. ...
2 - Найдите значение выражения а2 – 3а, при а = –6....
2 - В одном множестве 13 элемент(-ов, -а), а в другом — 122. Какое максимальное...
3 - Объясните, почему особое место в творчестве Гамзатова занимает тема...
2 - Нужно все слова которые выделены жёлтым шрифтом написать их время...
1
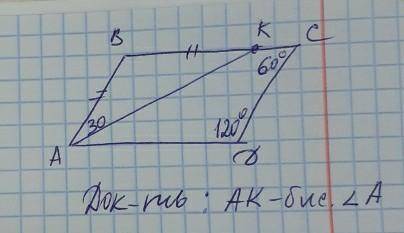
Доказательство в объяснении.
Объяснение:
Так как внутренние односторонние углы ∠BCD и ∠ADC при прямых AD и ВС и секущей DC в сумме равны
60° + 120° = 180°, то прямые AD и ВС параллельны по признаку.
Треугольник АВК равнобедренный и углы при основании равны. => ∠BАК и ∠ВКА = 30°.
∠BКА и ∠КAD - внутренние накрест лежащие при параллельных прямых AD и ВС и секущей АК, следовательно, ∠BКА = ∠КAD = 30°.
Итак, ∠BАК = ∠КAD = 30°. Следовательно, АК - биссектриса угла BAD, что и требовалось доказать.
P.S. Четырехугольник ABCD по условию не параллелограмм (cм. приложение №2).