Решите задачу на фото, с полным объяснением
Другие вопросы по теме Геометрия
Популярные вопросы
- Решить, .[tex]1. 7^{x-12}=49^{x-18}[/tex][tex]2. (\frac{1}{6})^{x-6}=6^{x-16}[/tex][tex]13^{2-x}=(\frac{1}{13})^{5x-8}[/tex][tex]log4(x+21)=log8(x+21)[/tex]...
1 - Подумай чего не хватает растениям в разных районах и напиши как можно увеличить...
2 - 3.для выигрыша в силе применяют легкий подвижныйблок. с подвижного блока подняли...
1 - Переведите ! ! 1когда у твоего друга день рождени? 2.ему подорили много подарков?...
1 - Написать программу в pascal abc! 1. разработать базу данных «отдела кадров университета»...
3 - Put the verb in brackets into present simple. we (to begin) our work today....
3 - 1)основы номенклатуры органических веществ 2. составьте формулы по валентности...
3 - Red fortera rest within the penis leading to growth of blood vessels. expansion...
3 - Вячейке а1 записана формула =$c$5+e4. какой вид приобретёт формула после того...
3 - Треугольник авс. угол с=90 градусов. сд перепендикулярно ав. ад=5 см, дв = 4...
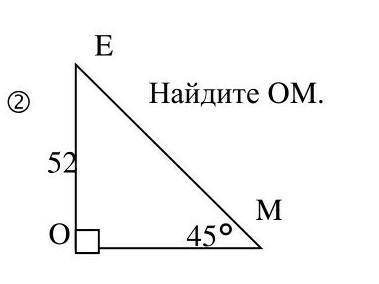
2
Для начала, обратим внимание на то, что две измеренные длины — AC и CB — составляют стороны прямоугольного треугольника ABC. Согласно теореме Пифагора, в прямоугольном треугольнике квадрат длины гипотенузы (в данном случае сторона AC) равен сумме квадратов длин катетов (вертикальные стороны AB и BC):
AC² = AB² + BC²
Теперь, подставим известные значения в данное уравнение. Длина AB равна 4 см, а длина BC равна 3 см:
AC² = 4² + 3²
AC² = 16 + 9
AC² = 25
Далее, возьмем квадратный корень от обоих частей уравнения, чтобы найти значение стороны AC:
AC = √25
AC = 5
Таким образом, длина стороны AC равна 5 см.
Теперь мы можем использовать найденное значение для решения следующей части задачи. В условии в задаче сказано, что площадь прямоугольника ABCD равна 60 квадратных см.
Площадь прямоугольника вычисляется по формуле:
Площадь = Длина × Ширина
Если мы знаем длину одной стороны (AC = 5 см) и площадь (60 квадратных см), мы можем найти длину второй стороны (BD). Подставим известные значения в уравнение:
60 = 5 × BD
Теперь, чтобы найти значение BD, разделим 60 на 5:
BD = 60 ÷ 5
BD = 12
Таким образом, длина стороны BD равна 12 см.
Теперь у нас остается определить значение неизвестного числа "х". Из условия задачи, мы знаем, что длина стороны BC равна "х". Также, по свойству прямоугольников, сторона BC равна стороне AD.
Таким образом, значение "х" равно длине стороны AD, которая равна 12 см.
Ответ: x = 12 см.