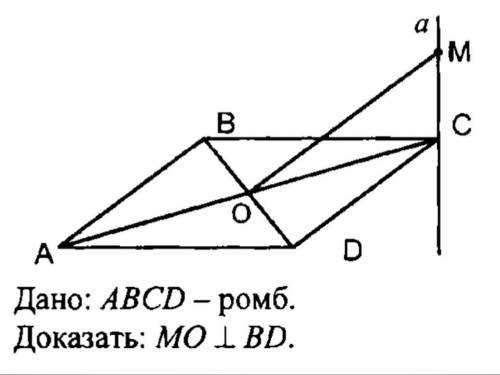
Решите задачу: Дано, что прямая α перпендикулярна плоскости АВС, АВСD - ромб.
Докажите, что МО⊥ВD
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.Признак,который не проявляется у гибридов первого поколения... Ограничивающий...
1 - Уявіть, що вам потрібно привітати з днем наро- дження бабусю. Поширте текст...
2 - Кількість опадів у тропічного пояса...
3 - Укажи жилище оседлых усуней...
2 - Приведите 3 факта, позволяющие говорить о взаимовлияние национальных культур...
3 - Сила 5*10-3 Н действует на массу 2*10-2 кг, прикрепленную к пружине, вызывает...
3 - Цитатна Характеристика Шерлока Холмса з,, Спілка Рудих,, ...
1 - Якщо об’єкт рухається з швидкістю 150000км/с, то як зміниться його розмір, що...
2 - На проводник сопротивленем R = 40 Ом подастся напряжение U= 80 В. Чему равна...
1 - 2х+11 = 3 2 мне , решить это уравнение . - это пробел ...
1
1. Изначально, у нас есть два даных: прямая α перпендикулярна плоскости АВС и АВСD - ромб.
2. В ромбе АВСD все стороны равны между собой. Значит, AD=AB.
3. Также, в ромбе АВСD все углы равны между собой. Значит, угол АВС равен углу ADS.
4. Так как прямая α перпендикулярна плоскости АВС, значит она перпендикулярна к любой прямой, лежащей в этой плоскости. В частности, это означает, что угол АВС равен углу МОD.
5. МОD - прямая.
6. Из пункта 4 углы АВС и МОD равны между собой.
7. Значит, угол ADS также равен углу МОD.
8. Однако в треугольнике ADS угол ADS равен 90 градусам, так как АВСD - ромб и каждый его угол равен 90 градусам.
9. Из пунктов 7 и 8 следует, что угол МОD также равен 90 градусам.
10. Следовательно, МО ⊥ ВD.
Таким образом, мы доказали, что МО⊥ВD на основе известных свойств и определений ромба и перпендикуляра.