Решите задачку по геометрии

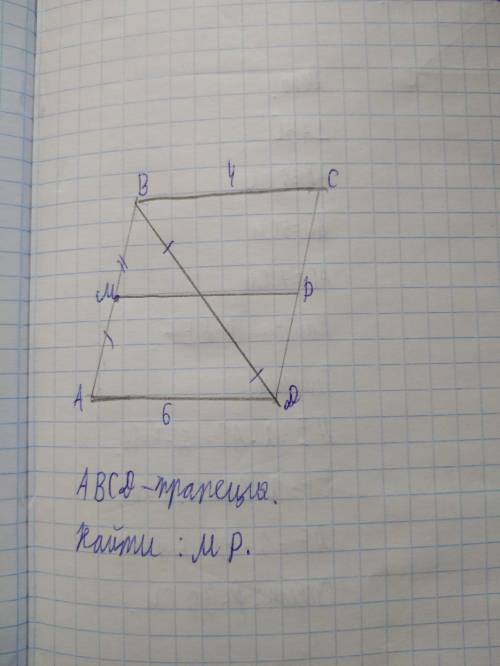
Обозначим на чертеже точку О – точку пересечения МР и BD.

ВО=OD по условию,

BM=MA по условию,

Тогда по обратной теореме Пифагора МО||AD так как прямые МО и AD делят стороны угла BD и BA на равные части.

Следовательно МР||AD так же.

Исходя из того что ВМ=МА: точка М – середина ВА.

Так как МР – отрезок, параллельный основанию AD трапеции ABCD, и при этом проходит через середину боковой стороны ВА – точку М, то МР – средняя линия трапеции ABCD.

Средняя линия трапеции равна полусумме оснований.

То есть МР=(ВС+AD)÷2=(4+6)÷2=5.

ответ: 5.