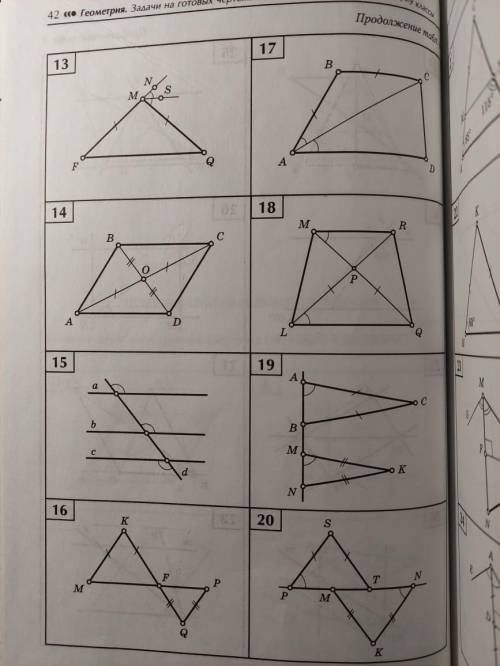
Решите задачи по рисунку №14, 15, 16, 17. Нужно сначала найти, а потом доказать параллельность прямых.

Хорошо, давайте решим задачи по рисунку №14, 15, 16 и 17 и докажем параллельность прямых.

Задача 14:
Мы видим две параллельные прямые (AB || CD) и три пересекающие их прямые (AC, AE и BD). Нам нужно найти значение углов x и y.

Посмотрим на треугольник AEB. Так как AB || CD, угол AEB является соответственным углом углу CDB. Это значит, что угол AEB = углу CDB = x.

Теперь посмотрим на треугольник ADC. Так как AB || CD, угол CDA является соответственным углу BAE. Это значит, что угол CDA = углу BAE = y.

Мы также видим, что углы внутри треугольника AEB должны суммироваться до 180 градусов. Значит, x + y + 90 = 180. Решим эту уравнение:

x + y = 90.

Таким образом, мы нашли значения углов x и y.

Задача 15:
Мы видим две параллельные прямые (AB || CD) и две пересекающие их прямые (AE и BD). Нам нужно найти значение углов x и y.

Посмотрим на треугольник ABC. Так как AB || CD, угол BAC является соответственным углом углу CDB. Это значит, что угол BAC = углу CDB = x.

Также посмотрим на треугольник BDA. Так как AB || CD, угол ABD является соответственным углу BAE. Это значит, что угол ABD = углу BAE = y.

Мы также видим, что углы внутри треугольника ABC должны суммироваться до 180 градусов. Значит, y + x + 90 = 180. Решим это уравнение:

x + y = 90.

Таким образом, мы нашли значения углов x и y.

Задача 16:
Мы видим две прямые, которые пересекаются в точке O. Нам нужно доказать, что прямые AB и CD параллельны.

Для доказательства параллельности двух прямых, нам необходимо установить, что соответствующие углы одинаковые.

Посмотрим на треугольник AOC. Угол AOC - внутренний угол, и он равен 180° - 120° = 60°.

Теперь посмотрим на треугольник DOB. Угол DOB - внутренний угол, и он равен 180° - 120° = 60°.

Таким образом, угол AOC = углу DOB. Мы доказали, что соответствующие углы равны, что означает, что прямые AB и CD параллельны.

Задача 17:
Мы видим две прямые, которые пересекаются в точке O. Нам нужно доказать, что прямые AD и BC параллельны.

Для доказательства параллельности двух прямых, нам необходимо установить, что соответствующие углы одинаковые.

Посмотрим на треугольник AOC. Угол AOC - внутренний угол, и он равен 180° - 120° = 60°.

Теперь посмотрим на треугольник BOC. Угол BOC - внутренний угол, и он равен 180° - 120° = 60°.

Таким образом, угол AOC = углу BOC. Мы доказали, что соответствующие углы равны, что означает, что прямые AD и BC параллельны.

Это были пошаговые решения задач по рисункам №14, 15, 16 и 17 с доказательством параллельности прямых. Надеюсь, что ясно объяснил. Если у вас есть еще вопросы, не стесняйтесь задавать. Я всегда готов помочь!