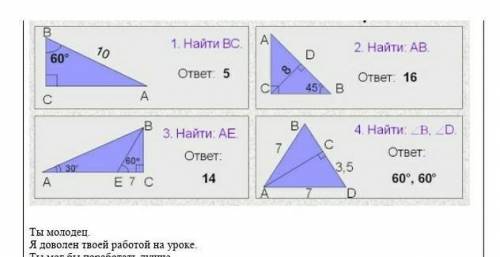
Решите задачи по готовым чертежам и ответам.
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение на тему моя любимая игрушка...
2 - По интонации предложения могут...
3 - Для чего деньги должны быть лёгкими и удобными в перемещении...
3 - Амени данные словосочетания словосочетанием прилагательное + существительное...
2 - Голубь с зайцем 5 кг, парасёнок с голубем 99 кг,три зайца 12кг.сколько весят...
1 - Тело движется прямолинейно. под действием постоянной силы величиной 4 н импульс...
3 - Найти формулу. дано: сумма 10. одно число,больше другого на 2. и 4. но,как...
1 - Выпишите формы рельефа образованные ледником ветром человеком...
2 - Сколько лет потребовалось человечеству чтоб оно стало личностью....
2 - Какое из четырех чисел является наименьшим? 1110101 в двоичной сис-ме 72 в...
3
Задача 1.
Найдем ∠А = 90°-60° = 30°.
Катет ВС находится напротив угла 30°, а значит, что он равен половине гипотенузы ВА, то есть 10:2=5.
ответ: ВС= 5.
Задача 2.
Найдем ∠А = 90°-45° = 45°.
Значит, ΔАСВ - равнобедренный, АС=СВ.
Высота равнобедренного треугольника, проведенная к основанию, является и биссектрисой угла.
∠САВ = ∠ДСВ = 90:2 = 45°.
Тогда ΔСДВ - равнобедренный.
СД= ДВ как боковые стороны.
АВ = АД+ДВ = 8+8 = 16
ответ: 16.
Задача 3.
∠ЕВС = 90-60=30°
катет ЕС равен половине гипотенузы ЕВ, тогда ЕВ = 7+7=14
∠АЕВ = 180-60=120°
∠АВЕ = 180-120-30 = 30° (∠АВЕ).
Тогда ΔАВЕ - равнобедренный,
основания АЕ=ЕВ = 14
ответ: АЕ = 14
Задача 4.
Так как АВ=АД = 7 (по условию), то ΔАВД - равнобедренный.
∠В=∠Д.
В ΔАСД катет СД = 3,5, то есть половине гипотенузы АД (которая равна 7). Из этого следует, что напротив стороны СД находится угол 30° (∠САД).
Соответственно, что ∠СДА = 60° (90°-30°=60°).
У равнобедренного треугольника углы при основании равны, значит
∠В = ∠Д = 60°.