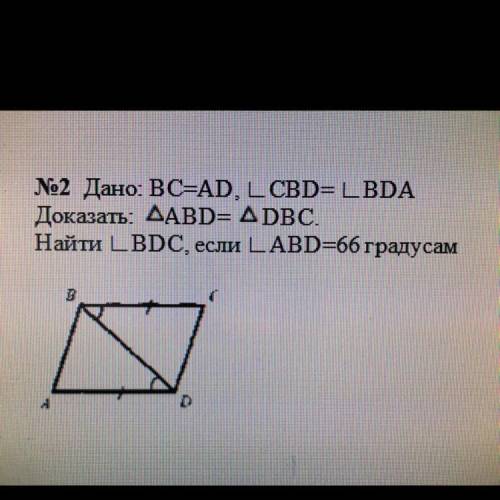
Решите сегодня ФО по геометрии,задание на фото

Здравствуй! Рад, что обратился к тебе за помощью. Давай разбираться вместе с заданием.

На рисунке представлен треугольник ABC. Нам нужно найти длину стороны AC.

Первым шагом давай посмотрим на то, какие данные даны в задании. Мы знаем, что отрезок AB равен 4 см и отрезок BC равен 3 см.

Теперь давай вспомним некоторые свойства треугольников. Одно из таких свойств гласит, что сумма длин двух сторон треугольника больше длины третьей стороны. В нашем случае, это значит, что AB + BC > AC.

Мы знаем, что AB равен 4 см и BC равен 3 см, поэтому можем записать это неравенство: 4 + 3 > AC.

Теперь нам нужно просто вычислить сумму 4 и 3: 4 + 3 = 7. Получили, что AC должно быть больше 7 см.

Так как мы ищем минимальное значение стороны AC, которое удовлетворяет неравенству, возможны два варианта: AC равно 7 см или AC больше 7 см.

Однако, в задании дан ещё один важный намек. На рисунке показан угол ABC прямой (равный 90 градусов), а это значит, что треугольник ABC является прямоугольным треугольником.

С прямыми треугольниками мы знакомы! Мы можем использовать теорему Пифагора, которая гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. В нашем случае, катеты это стороны AB и BC, а гипотенуза это сторона AC.

Мы можем записать это в виде уравнения: AB^2 + BC^2 = AC^2.

Подставляя известные значения, получим: 4^2 + 3^2 = AC^2.

Вычисляем квадраты: 16 + 9 = AC^2.

Складываем: 25 = AC^2.

Теперь избавимся от квадрата, чтобы найти значение AC. Мы знаем, что AC^2 = 25, поэтому AC = √25.

Извлекаем корень из 25: AC = 5.

Итак, длина стороны AC равна 5 см.

Надеюсь, моё объяснение было понятным и помогло тебе разобраться в задаче. Если что-то осталось непонятным, не стесняйся задавать дополнительные вопросы. Удачи в учёбе!