Решите решение не должно быть уравнением
Другие вопросы по теме Геометрия
Популярные вопросы
- Почему несчастья мерцаловых мы узнаём в середине рассказа...
1 - с музыкой слова из песни запишите название не знаю ре фа ми ре фа фа фа ми ре...
3 - До какой высоты можно поднять воду в трубке поршнем?...
1 - напиши до якои групи належить физична карта Австралии с вашего атласу А за Простор...
1 - определить что это за виды швов.. ...
3 - ребята! Тема урока: Борьба саков против Александра МакедонскогоВ 336 году до н.э....
1 - Прямоугольники R1 и R2, квадраты S1, S2, и S3 показано ниже, в совокупности образуют...
3 - 2-Бромбутан обработали водным раствором КОН. Какой продукт при этом образовался?...
1 - Найди и выпиши фамилии композиторов которые писали произведения на темы музыки...
3 - Сумму расходов на продажу и 1 если знаете 3...
3
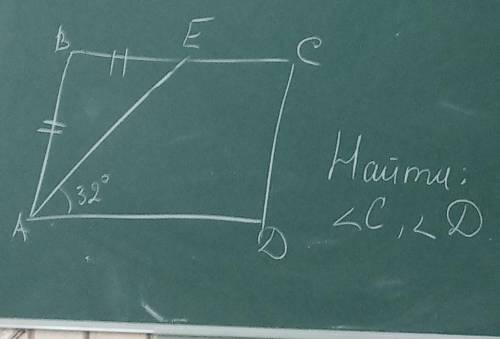
Если АВ=ВЕ по условию, то АЕ - биссектриса параллелограмма, которая отсекает равнобедренный ΔАВЕ.
Так как АЕ - биссектриса, то ∠ВАЕ=∠ЕАД = 32°.
Углы при основании равнобедренного ΔАВЕ равны,
значит ∠ВАЕ = ∠ВЕА = 32°.
Найдем ∠В = 180°-32°-32° = 116°.
Противоположные углы параллелограмма равны, тогда
∠В = ∠Д = 116°.
∠ВАД = 32°+32° = 64°.
∠А=∠С = 64°.
ответ: ∠С = 64°; ∠Д = 116°.