Решите если можно то побыстрей)
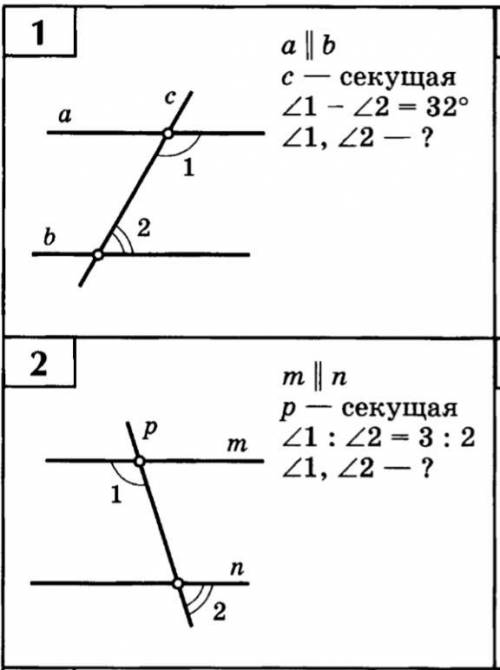
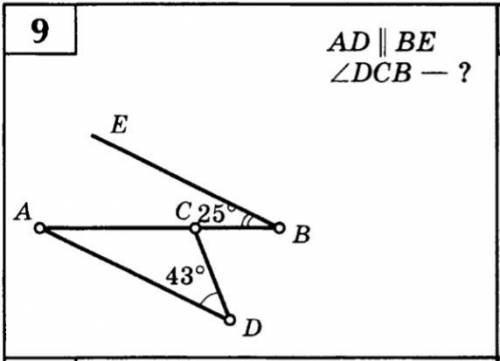
Другие вопросы по теме Геометрия
Популярные вопросы
- Выберите верные утверждения о химической активности элементов...
1 - Почему растворимость веществ увеличивается при повышении температуры?...
3 - 1. На карте Южной Америки (см. с. 155) найдите страны, граничащие...
2 - 5. Степень нагретости тел: а) теплоизоляция;6) температура;в)...
3 - 2 Complete the sentences with the past simple or past perfect...
2 - Complete the sentences. 1. One rule of thumb would be to dress...
2 - для кого из участников спора ОРУЩИЕ БАРАБАНЫ заглушают голос...
2 - Памагите решить мне иначе мама с крыши скинет...
2 - .«Шығамын тірі болсам адам болып» өлеңінің идеясына сай тармақты...
2 - Найдите нули функции у = х2 + 6х + 8...
3
По условию, нам дан прямоугольный треугольник ABC, где AC является гипотенузой, AB - одним катетом, а BC - другим катетом. Также, нам известно, что со сторонами прямоугольного треугольника связаны следующие пропорции:
AB:BC = 3:4
AB:AC = 4:5
Наша задача - найти отношение BC:AC. Для этого мы можем использовать свойство пропорций: если два отношения равны, то их взаимно обратные отношения равны.
Давайте найдем отношение BC:AB, используя первую пропорцию:
AB:BC = 3:4
BC:AB = 4:3
Затем, найдем отношение AC:AB, используя вторую пропорцию:
AB:AC = 4:5
AC:AB = 5:4
Теперь, мы можем объединить полученные отношения:
BC:AB = 4:3
AC:AB = 5:4
Для того чтобы найти отношение BC:AC, мы можем использовать правило перемножения пропорций. Перемножим числитель первого отношения и знаменатель второго отношения, а также числитель второго отношения и знаменатель первого отношения:
(BC:AB) * (AC:AB) = (4:3) * (5:4)
Проведя умножение, получаем:
BC * AC = 4 * 5
3 * 4
Теперь, давайте найдем произведение чисел 4 и 5:
BC * AC = 20
3 * 4
Осталось только найти значение отношения BC:AC, разделив числитель на знаменатель:
BC:AC = 20/(3 * 4)
Выполнив умножение в знаменателе, получаем:
BC:AC = 20/12
После сокращения, получаем окончательный ответ:
BC:AC = 5/3
Итак, мы нашли искомое отношение BC:AC, которое равно 5:3.