Решите две задачи. Геометрия 9 класс.
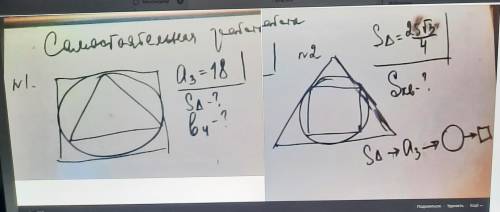
1. a3 = 18
S∆ -?
b4 - ?
2. S∆ = 25√3/4
S□-?
Чертежи и сами задания на фотографии.

1. Для решения первой задачи нам дано, что a3 = 18, где a3 - это сторона треугольника ∆. Мы должны найти площадь S∆ треугольника ∆ и сторону b4 треугольника ∆.

Для начала найдем сторону b4. Поскольку b4 - это сторона треугольника ∆, мы можем использовать теорему Пифагора, которая говорит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Из данных на чертеже видно, что a3 и b4 являются катетами прямоугольного треугольника. Значит, можем написать следующее:

a3^2 + b4^2 = c^2,

где c - это гипотенуза прямоугольного треугольника.

Мы знаем, что a3 = 18, так что можем заменить это значение в уравнение:

18^2 + b4^2 = c^2.

Теперь найдем гипотенузу с треугольника. Мы знаем, что a3 = 18, и на чертеже дано, что a3 = c. Поэтому c = 18.

Подставим это значение в уравнение:

18^2 + b4^2 = 18^2.

Упростим уравнение:

324 + b4^2 = 324.

Вычтем 324 из обоих сторон уравнения:

b4^2 = 0.

Возведем обе стороны в квадрат:

b4 = 0.

Таким образом, сторона b4 равна 0.

Теперь перейдем к нахождению площади S∆ треугольника ∆. Для этого мы можем использовать формулу площади треугольника, которая говорит, что площадь треугольника равна половине произведения длины основания на высоту.

Основанием треугольника является сторона a3, а высотой может служить перпендикуляр, опущенный из вершины треугольника на основание.

На чертеже видно, что перпендикуляр проходит через центр окружности с радиусом R = 5. Значит, этот перпендикуляр является радиусом окружности.

Мы знаем, что площадь треугольника ∆ равна половине произведения основания a3 на высоту (радиус R):

S∆ = (1/2) * a3 * R.

Мы уже знаем, что a3 = 18 и R = 5, поэтому можем подставить эти значения:

S∆ = (1/2) * 18 * 5 = 45.

Таким образом, площадь S∆ треугольника ∆ равна 45.

2. Для решения второй задачи нам дано, что S∆ = 25√3/4, где S∆ - это площадь треугольника ∆. Мы должны найти площадь S□ квадрата □.

На чертеже видно, что треугольник ∆ вписан в квадрат □. Значит, сторона квадрата □ равна стороне треугольника ∆.

Мы знаем, что площадь треугольника ∆ равна (√3/4) * (a3)^2, где a3 - это сторона треугольника ∆.

Мы знаем, что S∆ = 25√3/4, поэтому можем заменить это значение в уравнение:

25√3/4 = (√3/4) * (a3)^2.

Умножим обе стороны на 4/√3:

25 = a3^2.

Из этого уравнения мы можем найти сторону a3:

a3 = √25 = 5.

Таким образом, сторона треугольника ∆ (а также сторона квадрата □) равна 5.

Теперь мы можем найти площадь квадрата S□. Площадь квадрата равна квадрату длины его стороны, поэтому:

S□ = (5)^2 = 25.

Таким образом, площадь S□ квадрата □ равна 25.