1. Геометрия
  2. решить задачу. В равнобедренном

решить задачу. В равнобедренном треугольнике ABC, AC = BC, проведены CH - высота, AD - биссектриса, О - точка пересечения прямых СН и АD, внешний угол треугольника АВС при вершине С равен 124°. Найдите ∠АОС. Заранее благодарю

WaysWhite WaysWhite    1   14.08.2020 22:40    1

Ответы
Potterhead01 Potterhead01  15.10.2020 15:56

121°

Объяснение:

1-ый

\angel ACB=180-124=56

CH - биссектриса =>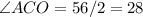 \angle ACO=56/2=28.

\angle CAB=124/2=62 => \angle CAO=62/2=31.

Тогда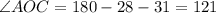 \angle AOC=180-28-31=121

Задача решена!

2-ой

Внешний угол треугольника равен сумме двух углов треугольника, которые не смежны с ним.

Поэтому верно:

\angle ACL=\angle ABC+\angle CAB

Т.к. треугольник равнобедренный, то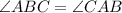 \angle ABC=\angle CAB.

Тогда:

\angle ACL=2\angle ABC

\angle ABC=\angle ACL/2

\angle ABC=124/2=62

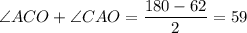Тогда \angle ACO+\angle CAO=\dfrac{180-62}{2}=59.

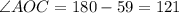
Значит \angle AOC=180-59=121

Задача решена!

ПОКАЗАТЬ ОТВЕТЫ
Айхан1111111111 Айхан1111111111  15.10.2020 15:56

Объяснение:см. во вложении


решить задачу. В равнобедренном треугольнике ABC, AC = BC, проведены CH - высота, AD - биссектриса,
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Texero Texero  24.09.2019 20:50
Найдите ребро куба если его диагональ равна 3√3 см...
alinaalya67 alinaalya67  24.09.2019 20:50
Из точки окружности проведены две перпендикулярные хорды, длины которых относятся как 5: 12. найдите длины хорд, если радиус окружности равен 13 см....
jrihdevhdve jrihdevhdve  24.09.2019 20:50
Найдите ребро куба если его диагональ равна 3√3 см. с дано...
jkazlova jkazlova  24.09.2019 20:40
Найти 3a*(a+2b),если |a|=4,|b|=3, (a,b)= 60 ( угол между векторами 60) ps тут с векторами...
daridasha57ү daridasha57ү  24.09.2019 20:40
Из точки а к окружности проведена секущая ав,внешняя и внутренняя части которой соответственно равны 9 и 16 см. найдите длину отрезка касательной,проведенной из точки а к...
kerimbaevazarema03 kerimbaevazarema03  24.09.2019 20:40
Впрямоугольном треугольнике аbc с гипотенузой ас угол с=30°.найдите биссектрису вк,если ск =8 корней из 2...
Машkа Машkа  24.09.2019 20:40
Дано треугольник abc, угол b=90°, угол ce-биссектриса, угол eb=8.см угол ec=16см. наити угол dac...
dorof077 dorof077  24.09.2019 20:40
Втреугольнике авс угол а - 120 градусов. радиус окружности, вписанной в треугольник, равен 10см. найдите расстояние от центра этой окружности до вершины а....
пистолетМакарова пистолетМакарова  24.09.2019 20:40
Из центра окружности о к хорде ав, равной 20см, проведён перпиндиккляр ос. найдите длину перпиндиккляра, если угол оав=45градусов. 15...
rast2k17 rast2k17  03.06.2019 09:40
Наименьшее расстояния от данной точки, расположенной вне окружности, до точек окружности равны соответственно 50 см и 20 см. найдите радиус данной окружности....

Популярные вопросы