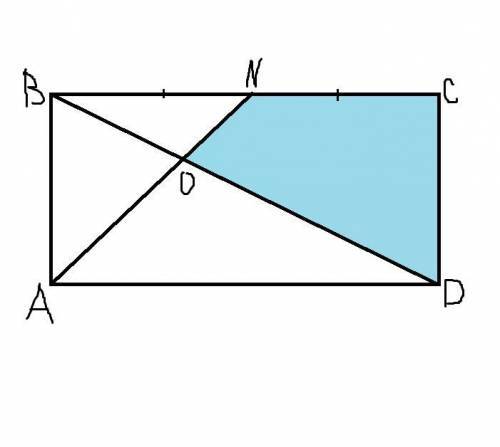
решить задачу по геометрии. ABCD - прямоугольник. Точка N - середина стороны BC. Отрезок AN пересекает диагональ BD в точке О. Найдите площадь четырёхугольника ONCD, если площадь прямоугольника ABCD равна 276.
ответ: 115
Нужен ход решения.
Даю готовый рисунок. Четырёхугольник, площадь которого нужно найти, закрашен голубым цветом.

Для решения данной задачи, нам потребуется использовать свойства прямоугольников и сходных треугольников.

1. Из условия задачи видно, что точка N является серединой стороны BC.
Обозначим точку пересечения отрезка AN с диагональю BD как точку О.

2. Рассмотрим треугольники ABO и DCO.
Они будут сходными, так как углы при основании AB и CD равны 90 градусам (так как ABCD - прямоугольник).
Кроме того, угол АОВ является вертикальным углом, и поэтому равен 90 градусам.

3. Если мы рассмотрим отношение сторон сходных треугольников, то оно будет равно отношению соответствующих сторон.
В данном случае, это будет отношение длины AO к длине DO:
AO/DO = AB/CD = 1/2 (так как N является серединой стороны BC).

4. Теперь мы можем использовать это отношение, чтобы найти длину отрезка DO.
Обозначим длину отрезка AO как x.
Тогда длина отрезка DO будет равна 2x, так как AO/DO = 1/2.

5. Площадь четырехугольника ONCD можно выразить как сумму площадей треугольников AON и DON.
Площадь треугольника AON равна (1/2) * x * AO.
Площадь треугольника DON равна (1/2) * 2x * DO.

6. Для нахождения площади четырехугольника ONCD, нам нужно сложить площади треугольников AON и DON:
S(ONCD) = (1/2) * x * AO + (1/2) * 2x * DO
= (1/2) * x * AO + (1/2) * 2x * 2x
= x * AO + 2x^2.

7. Мы знаем, что площадь прямоугольника ABCD равна 276.
Площадь прямоугольника ABCD можно выразить как произведение его двух сторон:
AB * BC = 276.

8. Мы также знаем, что точка N является серединой стороны BC.
То есть длина стороны BC будет равна 2 * BN.
Таким образом, мы можем переписать уравнение площади прямоугольника ABCD следующим образом:
AB * 2 * BN = 276.

9. Так как N является серединой стороны BC, то BN будет равно (1/2) * BC.
Подставим это значение в уравнение из пункта 8 для дальнейших вычислений:
AB * BC = 276,
AB * 2 * (1/2) * BC = 276,
AB * BC = 2 * 276,
AB * BC = 552.

10. Мы также знаем, что отношение AO к DO равно 1/2 (из пункта 3).
Таким образом, можно записать уравнение:
AO/DO = 1/2,
AO = (1/2) * DO.

11. Подставим в уравнение из пункта 9 значения AO и DO:
x * (1/2) * DO = x * (1/2) * 2x = x^2,
AB * BC = x^2,
552 = x^2.

12. Найдем значение x, возведя обе части уравнения в квадрат:
552^2 = x^4,
305,004 = x^4,
x ≈ 11.

13. Используя найденное значение x, можем найти площадь четырехугольника ONCD:
S(ONCD) = x * AO + 2x^2,
= 11 * 11/2 + 2 * 11^2,
= 121/2 + 242,
= 61 + 242,
= 303.

14. Ответом является площадь четырехугольника ONCD, которая равна 303.