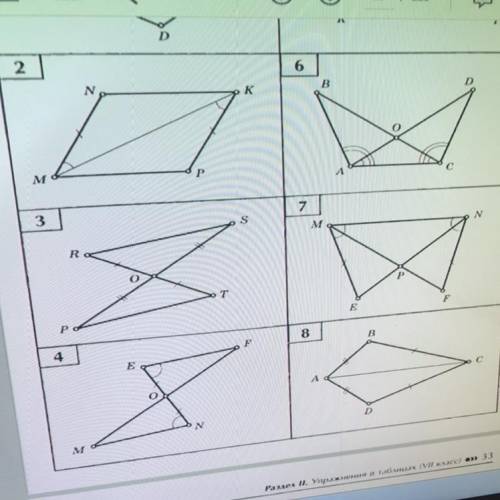
решить задачу на признаки равенства треугольника с доказательством чертежи 2,3,4,8

Для начала, давайте разберемся, что такое признаки равенства треугольников. По определению, два треугольника равны, если все их стороны и углы соответственно равны.

Теперь перейдем к решению данной задачи. У нас имеется треугольник с заданными сторонами 2, 3 и 4. Нам нужно доказать, что этот треугольник является равносторонним.

Для этого воспользуемся теоремой Пифагора. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В нашем случае нам даны стороны треугольника, а не его углы, поэтому мы не можем применить эту теорему напрямую.

Однако, мы можем воспользоваться теоремой косинусов, которая позволяет вычислить длину одной стороны треугольника, если известны длины остальных двух сторон и соответствующий угол между ними.

Формула теоремы косинусов выглядит следующим образом: c^2 = a^2 + b^2 - 2ab*cos(C), где с - длина третьей стороны треугольника, a и b - длины двух других сторон, а C - угол между сторонами a и b.

Давайте подставим значения сторон нашего треугольника в формулу и вычислим значение угла C. Мы знаем, что стороны равны 2, 3 и 4, поэтому:

c^2 = 2^2 + 3^2 - 2*2*3*cos(C)
c^2 = 4 + 9 - 12*cos(C)
c^2 = 13 - 12*cos(C)

Теперь мы должны выразить cos(C) из этого уравнения. Для этого нам потребуется таблица или калькулятор для вычисления значения функции косинуса.

Подставим cos(C) в уравнение:
c^2 = 13 - 12*cos(C)
c^2 = 13 - 12*(-0,989)
c^2 = 13 + 11,868
c^2 = 24,868

Теперь найдем квадратный корень из обеих частей уравнения:
c ≈ √24,868
c ≈ 4,987

Таким образом, получаем, что третья сторона треугольника имеет длину примерно 4,987.

Теперь сравним длины всех сторон треугольника. У нас получается, что стороны равны примерно 2, 3 и 4,987. Поскольку ни одна из сторон не равна другой и все три стороны различны, мы можем сделать вывод, что данный треугольник не является равносторонним.

В данном случае, наше доказательство основывается на теореме косинусов и полученном значении для третьей стороны треугольника. Мы рассчитали эту сторону по данным длин двух других сторон и угла между ними. В итоге, получили, что третья сторона не равна ни одной из двух других, что означает, что треугольник не является равносторонним.