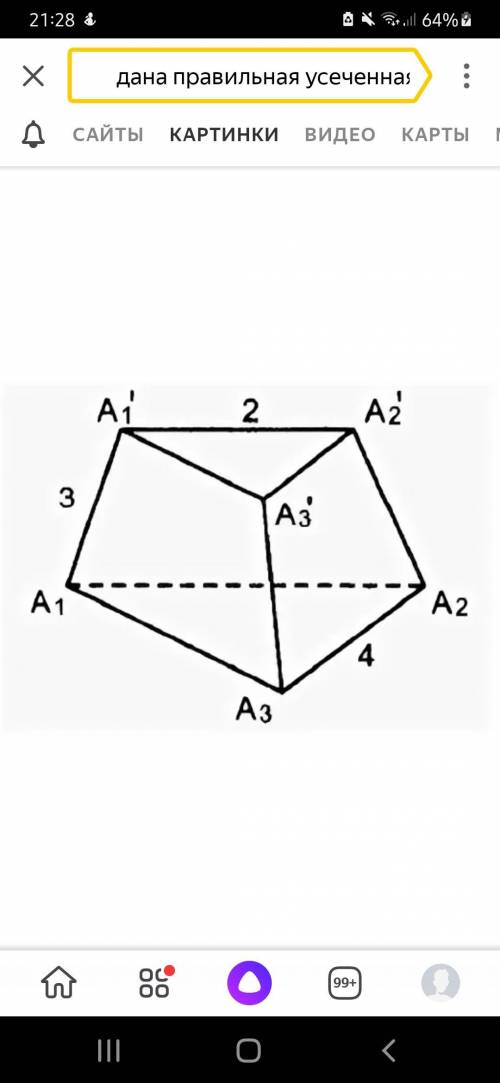
решить задачу Дана правильная усеченная пирамида. A1A1'=3 A3A2=4 A1'A2'=2

Найдите площадь полной поверхности.

Для решения этой задачи, мы должны найти площадь полной поверхности правильной усеченной пирамиды.

Для начала, нам необходимо понять структуру и свойства этой пирамиды.

Правильная усеченная пирамида имеет два основания, которые являются правильными многоугольниками. В данном случае, мы имеем два правильных треугольника - A1A1'A2' и A1A2A3.

Также в пирамиде есть боковые грани, которые представляют собой равнобедренные трапеции. В нашем случае, это грани A1A1'A2A3 и A1'A2'A3.

Площадь полной поверхности пирамиды состоит из площади обоих оснований (A1A1'A2' и A1A2A3) и площадей всех боковых граней.

Чтобы найти площадь боковой грани A1A1'A2A3, нам нужно найти площадь трапеции A1A1'A2A3.

Площадь трапеции можно найти по формуле: Площадь = (сумма оснований) * (высота) / 2.

В нашем случае, сумма оснований A1'A2' и A1A2 - это 2 + 4 = 6, а высота равна A1A1'.

Из условия задачи, мы знаем, что A1A1' = 3. Подставляя значения в формулу, получаем:

Площадь трапеции A1A1'A2A3 = (6 * 3) / 2 = 9.

Площадь боковой грани A1A1'A2A3 равна 9.

Теперь, чтобы найти площадь боковой грани A1'A2'A3, мы можем использовать такую же формулу площади трапеции.

Сумма оснований трапеции A1'A2'A3 равна A1'A2' + A2'A3. Из условия задачи, мы знаем, что A1'A2' = 2 и A2'A3 = 4.

Подставляя значения в формулу, получаем: Площадь трапеции A1'A2'A3 = (2 + 4) * A1'A2' / 2 = 6.

Площадь боковой грани A1'A2'A3 равна 6.

Наконец, чтобы найти площадь обоих оснований, мы можем использовать формулу площади треугольника.

Площадь треугольника можно найти по формуле: Площадь = основание * высота / 2.

В нашем случае, основание треугольника A1A1'A2' равно A1'A2' = 2, а высота равна A1A1' = 3.

Из условия задачи, мы знаем, что A1A1' = 3 и A1'A2' = 2. Подставляя значения в формулу, получаем:

Площадь треугольника A1A1'A2' = (2 * 3) / 2 = 3.

Площадь основания A1A1'A2' равна 3.

Точно так же, площадь треугольника A1A2A3 равна (4 * 3) / 2 = 6.

Площадь основания A1A2A3 равна 6.

Теперь мы можем найти площадь полной поверхности пирамиды, сложив площади обоих оснований и площади всех боковых граней:

Площадь полной поверхности = площадь основания A1A1'A2' + площадь основания A1A2A3 + площадь боковой грани A1A1'A2A3 + площадь боковой грани A1'A2'A3

Подставляя значения, получаем:

Площадь полной поверхности = 3 + 6 + 9 + 6 = 24.

Таким образом, площадь полной поверхности данной усеченной пирамиды равна 24 квадратных единиц.