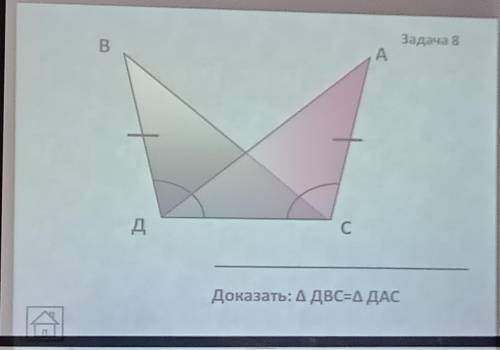
решить задачи по геометрии с условием по типу: дано и т.д.
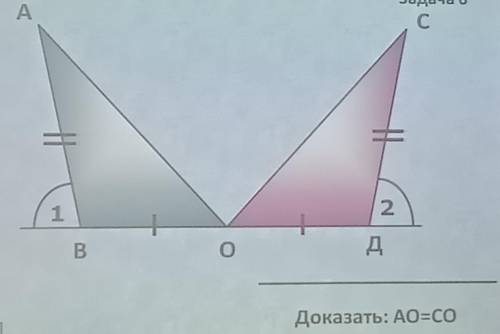
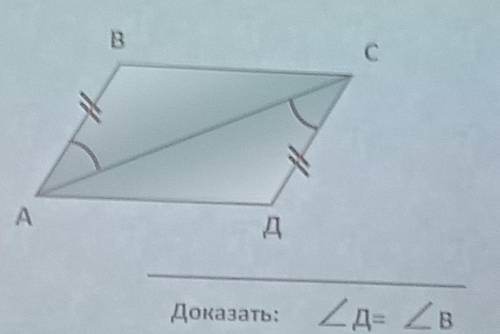
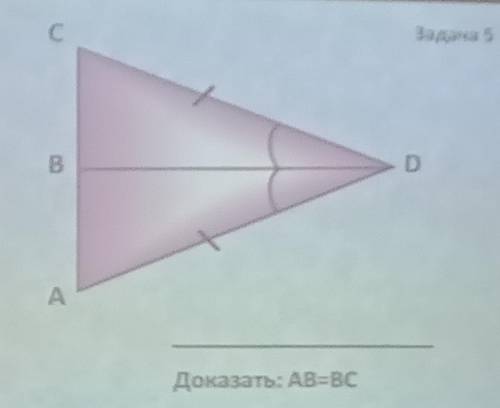
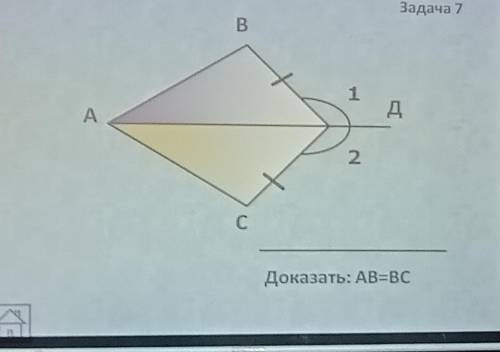
Ответы
Данная задача по геометрии заключается в том, чтобы найти значение неизвестной стороны прямоугольного треугольника. Для этого будем использовать теорему Пифагора и свойства прямоугольного треугольника.
Первая задача:
В задаче дано, что прямоугольный треугольник имеет одну сторону 3 см, а другую сторону 4 см. Мы должны найти длину гипотенузы треугольника.
Шаг 1: По теореме Пифагора, сумма квадратов катетов (сторон треугольника, не гипотенузы) равняется квадрату гипотенузы. Поэтому можем написать уравнение:
3^2 + 4^2 = x^2
Шаг 2: Решим уравнение:
9 + 16 = x^2
25 = x^2
Шаг 3: Извлечем квадратный корень из обеих сторон уравнения, чтобы получить значение x:
√25 = √x^2
5 = x
Ответ: Длина гипотенузы равна 5 см.
Вторая задача:
В данной задаче известны две стороны прямоугольного треугольника (катеты) - 8 см и 15 см. Мы должны найти длину гипотенузы.
Шаг 1: По аналогии с первой задачей, напишем уравнение по теореме Пифагора:
8^2 + 15^2 = x^2
Шаг 2: Решим уравнение:
64 + 225 = x^2
289 = x^2
Шаг 3: Извлечем квадратный корень из обеих сторон уравнения:
√289 = √x^2
17 = x
Ответ: Длина гипотенузы равна 17 см.
Третья задача:
В данной задаче задана длина стороны прямоугольного треугольника (катет) - 12 см, а длина гипотенузы - 13 см. Нам нужно найти длину второго катета.
Шаг 1: Также, используя теорему Пифагора, можем записать уравнение:
12^2 + x^2 = 13^2
Шаг 2: Решим уравнение:
144 + x^2 = 169
x^2 = 169 - 144
x^2 = 25
Шаг 3: Извлечем квадратный корень из обеих сторон уравнения:
√(x^2) = √25
x = 5
Ответ: Длина второго катета равна 5 см.
Надеюсь, что объяснение было понятным и полезным! Если у вас есть еще вопросы, не стесняйтесь задавать.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Поле прямо угольной формы имеет площадь 4 га его ширина 50см. вычислите...
3 - 34 напишите полное решение этого тригонометрического уравнения !...
3 - С! нужно сделать цепочку и 1)zncl2 -zn- zno- h2o- h2- hcl- cacl2 2) сколько...
1 - Найдите площадь прямоугоника если периметр прямоугоника равен 20 см, а...
1 - Лестница соединяет точки а и в.высота каждой ступени =14см,а длина=48см.расстояние...
3 - Вкаком ряду все прилагательные не имеют краткой формы и степени сравнения...
1 - Уверы 4 рубля.у ани 7 рублей.на сколько больше рублей у ани,чем у веры?...
3 - ты хочешь знать, что делал я на воле ? какой смысл вкладывает мцыри в...
2 - Весной самец волюшки строит гнездо, в котором самка должна отложить икру....
2 - Письмо другу на тему школьный праздник...
1