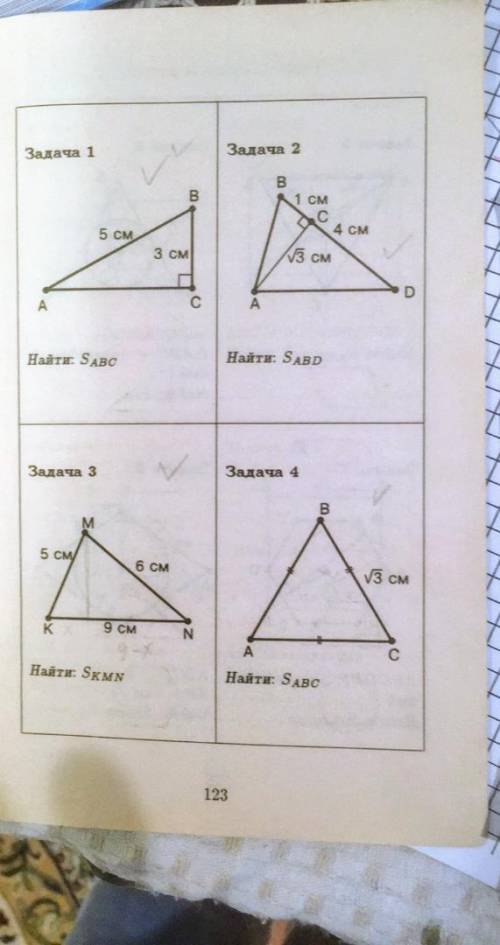
РЕШИТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ

ответ:надеюсь ты поймёшь мой почерк, аахахах

Объяснение:

Добрый день, уважаемый школьник! Я с удовольствием помогу вам решить задачи по геометрии.

Перейдем к рассмотрению задачи. Нам дано изображение треугольника ABC, в котором AB = AC = 8 см, а высота BD проведена из вершины B к отрезку AC. Мы должны найти длину отрезка BD.

Для того чтобы найти решение, мы можем использовать теорему Пифагора, говорящую о том, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

В данной задаче, треугольник ABC не является прямоугольным, но мы можем создать прямоугольный треугольник BDC по теореме о высоте треугольника.

Так как треугольник BDC — прямоугольный треугольник, мы можем применить теорему Пифагора к этому треугольнику. Катет BD будет одним из уголков этого треугольника, а катет DC — другим. Гипотенузой будет отрезок BC.

Таким образом, катет BD равен:
BD = √( BC² - DC²)

Теперь давайте рассмотрим отрезок DC. Он является катетом прямоугольного треугольника ADB, где А — это вершина прямоугольного треугольника, Мы знаем, что угол BDC прямой, так как BD — высота треугольника ABC. Значит, угол ADC тоже прямой.

Поскольку ABC — равносторонний треугольник, угол BAC = 60°. Также угол ADC — прямой, значит угол DAC будет 180° - 90° - 60° = 30°.

Теперь мы можем использовать тригонометрию для нахождения отрезка DC. Так как у нас есть два угла треугольника ADC, мы можем использовать формулу для тангенса:
tan(30°) = DC / AB

Подставляем известные значения и находим длину DC:
tan(30°) = DC / 8

Мы можем найти значение tangens 30°, которое равно √3 / 3.
Подставляем этот результат в уравнение:
√3 / 3 = DC / 8

Теперь нам нужно найти DC:
DC = (8 * √3) / 3

Теперь, когда у нас есть значения длин отрезков BC и DC, мы можем найти BD, используя формулу из начала решения:
BD = √( BC² - DC²)
BD = √(8² - [(8 * √3) / 3]²)

Теперь выполняем вычисления:
BD = √(64 - (64 * 3) / 9)
BD = √(64 - 192/9)
BD = √(384/9 - 192/9)
BD = √(192/9)
BD = 8 * √(2/9)

Итак, длина отрезка BD равна 8 * √(2/9) см.

Я надеюсь, что данное пошаговое решение помогло вам понять, как решить данную геометрическую задачу. Если у вас возникнут еще вопросы, не стесняйтесь задавать их. Я с удовольствием помогу!