Решить! в треугольнике klm отрезок км = 24,8 дм, угол м = 30 градусов, угол к = 90 градусов. найдите: 1)расстояние от точки к

Question

Геометрия: Решить! в треугольнике klm отрезок км = 24,8 дм, угол м = 30 градусов, угол к = 90 градусов. найдите: 1)расстояние от точки к до прмой lm; 2)проекцию наклонной lm на прямой kl. и еще одно : прямая, пересекая две параллельные прямые образует угол 30 градусов. длина отрезка между параллельными прямыми 17,6 дм. найдите расстояние между параллельными прямыми. решите хотя бы одно, но желательно оба. заранее огромное !

Пикантные · Answer

1) По теореме: В прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Построим высоту из прямого угла К, обозначим точку пересечения D. Имеем, что гипотенуза КM в прямоугольном треугольнике KDM равна 2 катетам КD, по условию она равна 24,8 дм, т.е. KD = 12,4 дм. (KD - это расстояние от точки К до гипотенузы). По теореме Пифагора найдем второй катет KL, это и будет проекция наклонной LM на прямую KL: Составим уравнение, обозначив KL = x, LM = 2x
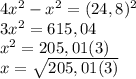
$4 x^{2} - x^{2} =(24,8)^{2} \\ 3 x^{2} =615,04 \\ x^{2} =205,01(3) \\ x= \sqrt{205,01(3)}$

Популярные вопросы