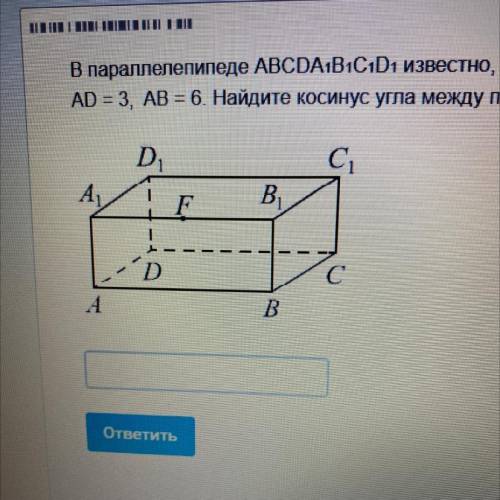
решить В параллелепипеде АВСDA1B1CD1 известно, что ABCD-прямоугольник, ребро АА1 перпендикулярно плоскости АВС, АА1= 7 из под корня, АD=3, АВ=6. Найдите косинус угла между прямыми DF и ВС, где F-середина А1В1
Другие вопросы по теме Геометрия
Популярные вопросы
- С одной вершины тупого угла паралеллограмма проведена биссектриса этого...
2 - Одинаковы ли молекулы воды, льда водяного пара? Почему не соединяются два...
1 - Задание 1 ( ). Сделайте схематический рисунок своего домашнего компьютера....
2 - В каком произведение Пушкина что-то упоминается о движении...
2 - 10. Зону всасывания корня визуально можно отличить по...
3 - Спишите. Графически объясните выбор гласной а или о. Как вы понимаете смысл...
1 - Для охлаждения воды можно использовать кусок льда, взятого при температуре...
2 - 1)Choose the right variant: ...help me? I m lost. A) You can; B)Can you;...
3 - Вкажіть сполуки з йонним йонним зв язком. а) 02 В)ВаCI2 б) SO3 Г) N2...
1 - Складіть перелік заходів, яких необхідно вжити в Україні для становлення...
1
Для начала, обратим внимание на то, что ребро АА1 перпендикулярно плоскости АВС, значит оно является высотой этой плоскости.
Так как АА1 = 7, а площадь прямоугольника ABCD равна АВ * AD (S = AB * AD), а значит S = 6 * 3 = 18, то по формуле площади прямоугольника, высота (ребро) АА1 является здесь 18/7 раза площади одного из ребер АВ или AD. Выберем AD, т.к. у нас уже известна эта сторона.
Теперь рассмотрим треугольник АА1D прямоугольной геометрической фигуры ABCD. В этом треугольнике одна из сторон равна 3, другая сторона равна 18/7, а гипотенуза - ребро АА1.
Воспользуемся теоремой Пифагора в этом треугольнике:
АА1^2 = AD^2 + А1D^2
АА1^2 = 3^2 + (18/7)^2
АА1^2 = 9 + (324/49) = (441+324)/49 = 765/49
АА1 = √(765/49)
Так как нам нужно найти косинус угла между прямыми DF и BC, то нам потребуется информация о длине этих прямых.
Для дальнейшего решения, обратим внимание на факт, что ВС и ED - параллельные прямые, ведь они параллельны боковым ребрам параллелепипеда.
Также обратим внимание, что ВС и EF - это противоположные стороны параллелограмма, а значит, они равны.
Теперь у нас есть равные стороны БС и ЕС, а также связь между диагоналями параллелограмма и параллелепипеда. Обозначим длину диагонали параллелограмма А1B1 как d, тогда EF = d/2.
В соответствии с теоремой Пифагора, можно записать следующее:
EF^2 + А1F^2 = А1Е^2
(d/2)^2 + (AF)^2 = (6√2)^2
(d/2)^2 + (AF)^2 = 36 * 2
(d/2)^2 + (AF)^2 = 72
(d/2)^2 + (AF)^2 = 72
AF^2 = 72 - (d/2)^2
AF = √(72 - (d/2)^2)
Теперь у нас есть значение длины прямой AF, где F - середина отрезка А1В1.
Для определения косинуса угла между прямыми DF и ВС, нам нужно знать длины их сторон.
Для начала, найдем длину отрезка DF. DF является диагональю параллелограмма А1B1C1D1. Обозначим длину DF как x.
Используя теорему Пифагора, мы можем записать:
DF^2 = (AB1)^2 + (AF)^2.
(x)^2 = (AA1 + A1B1)^2 + (AF)^2.
(x)^2 = (√(765/49) + √(d^2 + (d/2)^2))^2 + (√(72 - (d/2)^2))^2
Теперь у нас есть выражение для длины DF в зависимости от d.
Далее, найдем длину стороны ВС. ВС также является диагональю параллелепипеда. Обозначим длину ВС как у.
Используя теорему Пифагора в треугольнике ВСД, мы получим:
BC^2 = BD^2 + CD^2.
y^2 = (AD + DD1)^2 + (AA1 + (AB1 + BD1))^2
y^2 = (3 + 3)^2 + ((√(765/49) + √(d^2 + (d/2)^2)) + (6√2 + ВD1))^2
Наконец, мы можем найти косинус угла между прямыми DF и ВС, воспользовавшись формулой косинуса:
cos(φ) = (x^2 + y^2 - DF^2)/(2xy).
cos(φ) = ((√(765/49) + √(d^2 + (d/2)^2))^2 + (√(72 - (d/2)^2))^2 - x^2)/(2((√(765/49) + √(d^2 + (d/2)^2))(√(9+6√2+ВD1)^2)).
Таким образом, мы можем найти косинус угла между прямыми DF и ВС, используя указанные формулы и оценивая значения d, x и y в них.