решить!
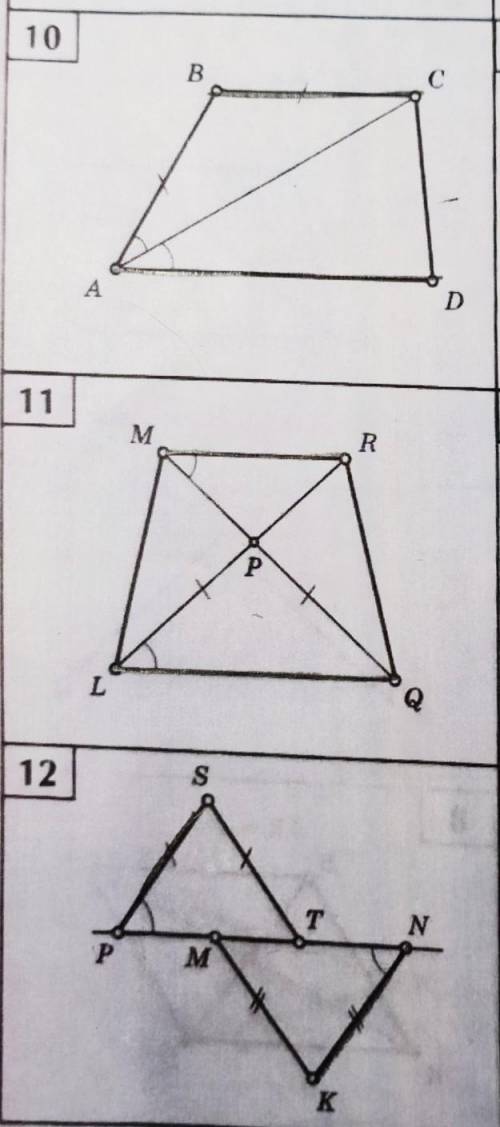
Укажите пары параллельных прямых и докажите их параллельность. ​

Для решения данной задачи сначала нужно определить, какие прямые в данном рисунке являются параллельными. Параллельные прямые – это прямые, которые никогда не пересекаются, даже при продлении.

На данном рисунке мы видим две пары прямых, которые выглядят параллельными: AB и CD, а также BC и AD. Для доказательства их параллельности, мы можем использовать несколько методов.

Метод 1: Использование свойств углов.

1. Рассмотрим угол ACB и угол CDA. Эти углы оба вершины направлены в одну сторону и лежат на смежных сторонах прямой CD (так как оба угла имеют общую вершину и лежат на смежных сторонах – это требование параллельности).
2. Далее, рассмотрим углы BAC и ACD. Они также вершины направлены в одну сторону и лежат на смежных сторонах прямой AB.
3. Если у нас есть две пары углов, удовлетворяющие условиям, это говорит о параллельности прямых AB и CD.

То же самое мы можем проделать для параллельности прямых BC и AD, сравнив углы CBD и BDA, а также углы BCA и BAD.

Метод 2: Использование свойств параллельных линий.

1. Рассмотрим угол BAC и угол CDA. Если прямые AB и CD параллельны, то углы BAC и CDA будут соответствующими углами и равны.
2. Далее, рассмотрим угол ACB и угол ACD. Если прямые AB и CD параллельны, то углы ACB и ACD будут вертикальными углами и равны.
3. Если у нас есть две пары углов, удовлетворяющие условиям, это говорит о параллельности прямых AB и CD.

То же самое мы можем проделать для параллельности прямых BC и AD, сравнив углы BCA и BAD, а также углы CBD и BDA.

Итак, используя свойства углов и прямых, мы можем утверждать, что прямые AB и CD, а также BC и AD являются параллельными.