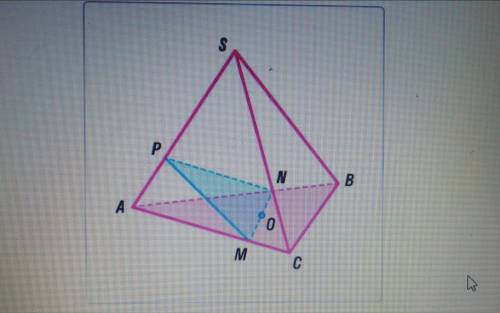
РЕШИТЬ! Точка о является центром грани авс правильного тетраэдра Sabc с ребром 3. Найдите площадь сечения.

Чтобы решить задачу, нам понадобится знать некоторые свойства тетраэдра и секущей плоскости.

Тетраэдр - это многогранник, состоящий из четырех треугольных граней. В данном случае, у нас есть правильный тетраэдр Sabc, что означает, что все его грани являются равносторонними треугольниками.

Дано, что точка О является центром грани авс тетраэдра. Это означает, что отрезки Оа, Оb и Ос являются медианами треугольника abc, а точка О - точкой пересечения этих медиан.

Найдем площадь сечения между плоскостью, проходящей через точку О и параллельной грани Sbc и плоскостью Sabc.

Шаг 1: Найдем высоту треугольника abc (h).

Так как треугольник равносторонний, то высота будет проходить через вершину а и образовывать прямой угол с основанием bc.

Зная, что треугольник abc правильный, можно использовать свойства равносторонних треугольников и высота будет равна (√3/2) * a, где а - длина основания треугольника.

Длина основания треугольника равна длине ребра тетраэдра, поэтому a = 3.

Таким образом, h = (√3/2) * 3 = (3√3) / 2.

Шаг 2: Найдем площадь грани Sbc (Sbc).

Так как треугольник Sbc равносторонний, его площадь можно найти с помощью формулы: Sbc = (a^2 √3) / 4, где а - длина стороны равностороннего треугольника.

В случае нашего тетраэдра, длина стороны (а) равна длине ребра, то есть а = 3.

Таким образом, Sbc = (3^2 √3) / 4 = (9√3) / 4.

Шаг 3: Найдем площадь сечения.

Площадь сечения будет равна площади треугольника aОb (Sab).

Так как Оа - это медиана треугольника abc, она делит этот треугольник пополам. Также, так как треугольник abc равносторонний, то треугольник Оbc также будет равносторонним.

Это значит, что у нас есть равносторонний треугольник Sab со стороной Оb длиной 3/2 и высотой h (половиной высоты треугольника abc).

Площадь равностороннего треугольника можно найти с помощью формулы: Sab = (a^2 √3) / 4, где а - длина стороны равностороннего треугольника.

В нашем случае, длина стороны (а) равна 3/2.

Таким образом, Sab = ((3/2)^2 √3) / 4 = (9√3) / 16.

Итак, площадь сечения между плоскостью, проходящей через точку О и параллельной грани Sbc, и плоскостью Sabc равна (9√3) / 16.