решить! Тема: Стереометрия. 10 класс. Перпендикулярность прямой и плоскости. ​

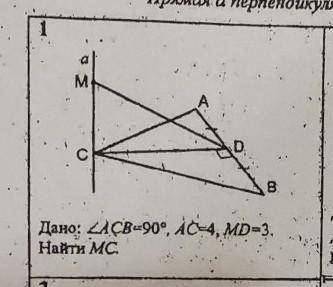
Чтобы решить эту задачу, нам необходимо разобраться в понятии перпендикулярности прямой и плоскости и применить соответствующие свойства стереометрии. Для начала, давайте определимся с понятием перпендикулярности. Если две линии или поверхности пересекаются под прямым углом (90 градусов), то они называются перпендикулярными. Одна из них является прямой, а другая - плоскостью. В данной задаче мы имеем сечение плоскости данным объемом - это треугольник ABC. Наша задача - найти прямую, которая перпендикулярна этой плоскости. Для решения этой задачи мы можем воспользоваться свойством, что прямая, параллельная одной из сторон треугольника, перпендикулярна плоскости, которую этот треугольник ограничивает. На рисунке мы видим, что одна из сторон треугольника ABC - это основание BC, а она параллельна данной прямой. Следовательно, чтобы найти прямую, перпендикулярную данной плоскости, нам нужно найти прямую, параллельную стороне BC треугольника ABC. Итак, чтобы найти прямую, параллельную стороне BC, мы можем провести линию DE, параллельную стороне BC и проходящую через точку D. Для этого нам необходимо найти эту точку D. Так как ABC - равнобедренный треугольник (два равных угла при основании), то медиана BD будет одновременно и высотой. Таким образом, высота проводится из вершины A перпендикулярно основанию BC и пересекает его в точке D. Таким образом, мы нашли точку D, которая является точкой пересечения медианы BD и основания BC. Теперь мы можем провести прямую, параллельную стороне BC, через точку D. Эта прямая будет перпендикулярна плоскости, которая ограничивает треугольник ABC. Представленное на рисунке решение является примером только для данной конкретной задачи, но мы можем использовать аналогичный метод для нахождения перпендикулярной прямой для других сечений плоскости. Надеюсь, данное пошаговое решение помогло вам понять, как найти прямую, перпендикулярную плоскости, используя заданный объем и геометрические свойства стереометрии.