Решить! сторона правильной треугольной пирамиды равна 4 см, а угол между боковым ребром и основанием равен 60·. найдите площадь полной поверхности пирамиды.
Ответы
Пусть треугольник ABC-основание пирамиды, он правильный, D верхняя вершина пирамиды. Рассмотрим треугольник DAB, он равнобедренный (т.к. призма правильная). По условию угол DAB равен 60 гр, значит треугольник DAB правильный, и значит призма состоит из 4 равных правильных треугольников, стороны которых равны 4. Найдем площадь одного из них, например, DAB. Высота DH =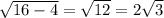 Площадь треугольника равна 4·2√3·1/2=4√3 Тогда площадь призмы равна 16√3
Площадь треугольника равна 4·2√3·1/2=4√3 Тогда площадь призмы равна 16√3
ПОКАЗАТЬ ОТВЕТЫ
 Площадь треугольника равна 4·2√3·1/2=4√3 Тогда площадь призмы равна 16√3
Площадь треугольника равна 4·2√3·1/2=4√3 Тогда площадь призмы равна 16√3
Другие вопросы по теме Геометрия
Популярные вопросы
- Что общего между операми иван сусанин и князь игорь ?...
3 - 7класс. 1. как взаимодействуют между собой молекулы ? 2. когда заметнее...
3 - Олицетворение в рассказе «стеклянный пруд»...
1 - Впишите,вставляя,где нужно, ь. объясните правописание слов. , ,...
3 - Посоветуйте интересные книги. мои любимые: карл саган - космос макс...
1 - Сочинение описание личности одноклассника по собственным наблюдениям...
3 - Где звёздочки надо вставить цифры, чтобы получился пример в столбик....
1 - Скласти складне речення зі словом хліб...
1 - Подобрать стих к грустной песне чейковского...
2 - Начертите коордианатный луч и отметье на нем точки соответствующие...
2