решить. Решение с полным объяснением.

Объяснение:

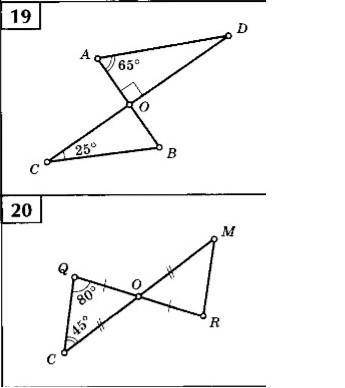
19) Рассмотрим треугольник АОD - прямоуг.

Угол О = 90 градусов

Угол D = 90 - 65 (угол А) = 25 градусов (сумма острых углов в прямоугольном треугольнике)

Или

Угол D = 180 - 90 - 65 = 25 градусов

Рассмотрим треугольник СОВ.

Угол AOD = угол COB = 90 градусов (верт.)

Угол ОВС = 180 - 90 - 65 = 25 градусов

Угол В = 180 - 90 - 25 (угол ОВС) = 65 градусов

20) Рассмотрим треугольник QOC.

Угол QOC = 180 - Угол Q - угол С = 180 - 80 - 45 = 55 градусов

Рассмотрим треугольники QOC и MOR.

QO = OR

CO = OM

Угол QOC = угол MOR (верт.) = 55 градусов =>

Треугольники равны по I признаку равенства треугольников (2 стороны и угол между ними) =>

угол Q = угол R = 80 градусов

Угол С = угол М = 45 градусов

Объяснение:

19) ΔADO и ΔСВО прямоугольные - ∠О=90° (вертикальные) ⇒ ∠D=90-65=25°, ∠B=90-25=65°.

20) ΔCQO и ΔMRO равны по двум сторонам (QO=RO и CO=MO по условию) и углу между ними (∠О вертикальный). В равных треугольниках соответственные углы равны: ∠Q=∠B=80°, ∠C=∠M=45°, ∠O=180-(80+45)=55° (сумма углов треугольника).