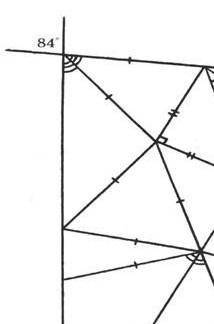
решить паутину по геометрии 7 класс​

.......................................................................................................................

Для решения данной задачи нам потребуется применить основные правила геометрии, такие как свойства треугольника, свойства равенства углов, а также правило внутренних и внешних углов многоугольника.

Итак, допустим, что точка O - центр окружности. Нам нужно найти значение угла AOB. Обратите внимание, что угол AOB - это центральный угол, стоящий на выпуклой дуге AB.

1. Заметим, что треугольник AOB - равнобедренный, так как AO и BO равны радиусам окружности. Поэтому угол OAB и угол OBA равны между собой.

2. Также мы знаем, что сумма углов треугольника равна 180 градусам. Поскольку угол OAB и угол OBA равны между собой, то мы можем записать уравнение: OAB + OBA + AOB = 180.

3. Подставим значение угла OAB вместо угла OBA. Так как угол OAB равен 64 градусам, мы можем записать: 64 + 64 + AOB = 180.

4. Теперь решим полученное уравнение: 128 + AOB = 180. Вычтем 128 из обеих частей уравнения: AOB = 180 - 128 = 52 градуса.

Итак, ответом на задачу будет то, что угол между лучами AO и BO (угол AOB) равен 52 градусам.