РЕШИТЬ ! Параллельны ли прямые а и b? Подробное решение с дано.

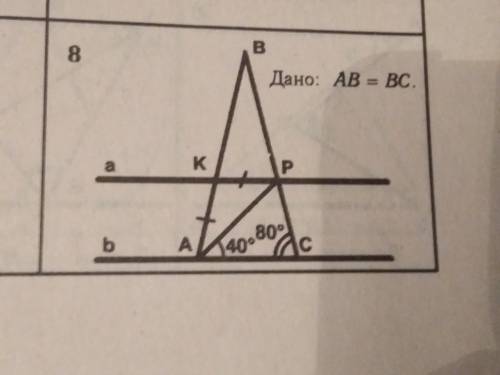
Дано: ABC, AB = BC, KA = KP, угол PAC = 40°, угол PCA = 80°.

AB = BC по условию => треугольник ABC - равнобедренный => угол BAC = 80°. Угол KAP = угол BAC - угол PAC = 40°. KA = KP => угол KAP = углу KPA = 40°. Угол KPA = углу PAC, а они накрест лежищие => a || b.

Для определения, параллельны ли прямые а и b, необходимо провести анализ углов и коэффициентов наклона данных прямых. Дано два уравнения прямых:

а: y = -2x + 4
b: y = -2x + 7

Чтобы убедиться, что прямые параллельны, проверим их углы и наклоны.

1. Проверка углов:
Прямые а и b параллельны, если их углы наклона равны или сумма углов наклона равна 180 градусам.
Углы наклона равны коэффициентам, стоящим перед x в уравнениях прямых.

Угол наклона прямой а: -2
Угол наклона прямой b: -2

Видим, что углы наклона прямых а и b равны, значит, можем сделать первый вывод, что прямые параллельны.

2. Проверка наклона:
Один из способов определить, параллельны ли прямые, заключается в сравнении их наклонов.
Если наклоны прямых a и b равны, то они параллельны.
Наклон прямой можно определить, исследуя коэффициент перед x в уравнении прямой.

Наклон прямой а: -2
Наклон прямой b: -2

Так как наклоны прямых а и b равны, можем сделать второй вывод, что прямые параллельны.

Таким образом, исходя из данного решения, мы можем заключить, что прямые a и b параллельны.