Решить! основанием прямой призмы abcda1b1c1d1 является параллелограмм abcd со сторонами 6 см и 6√3 см и углом 150·. диагональ b1d1 призмы образует с плоскостью основания угол в 60·. найдите площадь полной поверхности призмы.
Ответы
Предположим, что диагональ B1D образует угол с основанием 60гр. Найдем диагональ BD= 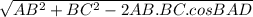 =6 УголBB1D=30гр, сл-но, B1D=2BD=12, ⇒BB1=6√3 Площадь основания равна AB·BC·sinBAD=18√3 Площадь AA1B1B=AB·BB1=36√3 Площадь AA1D1D=6√3·6√3=108 Получаем площадь полной поверхности =2·18√3+2·36√3+2·108=108√3+216=108(√3+2)
=6 УголBB1D=30гр, сл-но, B1D=2BD=12, ⇒BB1=6√3 Площадь основания равна AB·BC·sinBAD=18√3 Площадь AA1B1B=AB·BB1=36√3 Площадь AA1D1D=6√3·6√3=108 Получаем площадь полной поверхности =2·18√3+2·36√3+2·108=108√3+216=108(√3+2)
ПОКАЗАТЬ ОТВЕТЫ
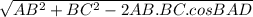 =6 УголBB1D=30гр, сл-но, B1D=2BD=12, ⇒BB1=6√3 Площадь основания равна AB·BC·sinBAD=18√3 Площадь AA1B1B=AB·BB1=36√3 Площадь AA1D1D=6√3·6√3=108 Получаем площадь полной поверхности =2·18√3+2·36√3+2·108=108√3+216=108(√3+2)
=6 УголBB1D=30гр, сл-но, B1D=2BD=12, ⇒BB1=6√3 Площадь основания равна AB·BC·sinBAD=18√3 Площадь AA1B1B=AB·BB1=36√3 Площадь AA1D1D=6√3·6√3=108 Получаем площадь полной поверхности =2·18√3+2·36√3+2·108=108√3+216=108(√3+2)
Другие вопросы по теме Геометрия
Популярные вопросы
- Дан невесомый рычаг, на одной стороне которого находятся два...
3 - Укріплені поселеннях слов ян називалися А) містами Б) городищами...
3 - Задание 1. Расставьте знаки препинания, подчеркните грамматические...
2 - Вкажіть вираз, тотожно рівний вираху 2x +4 - 6: А) 4 + 4x; Б)...
3 - What did the Tate Museum use to be?a theatrean old power stationA...
2 - Лабораторная работа. СБОРКА ПРОСТЕЙШЕГО ЭЛЕКТРОМАГНИТАИ ИСПЫТАНИЕ...
1 - Распределите следующие продукты питания с высоким содержанием...
3 - Изучите предложенное изображение и определите виды оглавлений....
3 - Кто написал повесть Яма и когда?...
1 - Listening Task 1. Listen to the conversation and fill in the...
1