решить, очень В единичном кубе a...d1 найдите угол между прямыми bb1 и a1c
Другие вопросы по теме Геометрия
Популярные вопросы
- Какое из этих изменений являеться самым важным в истории человечества...
2 - Используя чертеж найдите координаты точки А...
3 - А) при каком значении цифры * число38577* будет делиться на 2? Б) при каком значении...
1 - Скорость скворца равна, примерно 72 км/ч переведите в м/с...
1 - Упражнение 98. Вставьте обособленные определения в нужной форме в предложения из...
2 - Үйдө баарынын өз-өзүнчө бөлмөсү болуш керекпи? Эмне үчүн?...
1 - Производительность установки получения этилхлорида жидкофазным гидрохлорированием...
1 - Тание 3.Вычислите 1) -5/7+4/72) 5/12+(-1/12)3) (-1/6)+14) 5/16+(-1/16)5) (-4) +...
2 - Особенности битвы на реке Марне?...
2 - Задание. Составить Синквейн «Маргулан»Используя биографию и материалы §14-15 ,стр...
2
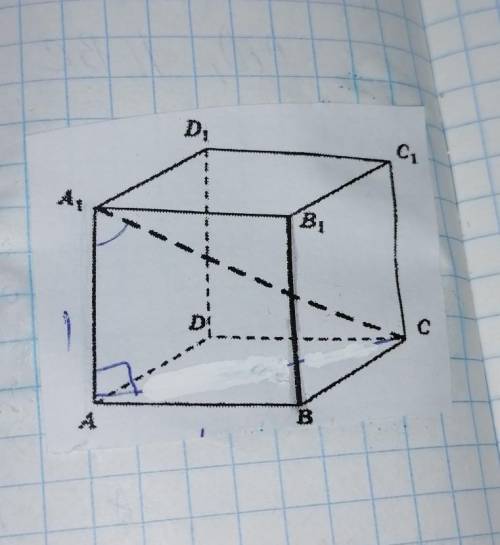
Для начала, посмотрим на изображение, чтобы понять геометрическую конфигурацию.
На изображении есть единичный куб с вершинами a, b, c и d. Мы должны найти угол между прямыми bb1 и a1c.
Прежде чем продолжить, давайте проанализируем задачу.
Угол между прямыми определяется как угол между их направляющими векторами. То есть, чтобы найти угол, нам нужно знать направления прямых.
Теперь давайте сосредоточимся на построении направляющих векторов прямых bb1 и a1c.
Прямая bb1 - это отрезок, соединяющий точки b и b1. Вектор направления этой прямой можно найти, вычитая координаты точки b из координат точки b1.
Вектор направления прямой bb1 = (b1x - bx, b1y - by, b1z - bz).
Аналогично, вектор направления прямой a1c = (c1x - ax, c1y - ay, c1z - az).
Теперь мы можем найти векторы направления для обеих прямых.
Для примера давайте примем координаты точек:
a = (1, 0, 0)
b = (0, 1, 0)
b1 = (0, 1, 1)
c = (1, 1, 0)
c1 = (2, 2, 0)
Теперь запишем векторы направления для прямых:
bb1 = (0 - 0, 1 - 1, 1 - 0) = (0, 0, 1)
a1c = (2 - 1, 2 - 1, 0 - 0) = (1, 1, 0)
Теперь, чтобы найти угол между двумя векторами, мы можем использовать формулу для нахождения косинуса угла между векторами:
cos(θ) = (bb1 • a1c) / (|bb1| * |a1c|),
где bb1 • a1c - это скалярное произведение векторов bb1 и a1c,
|bb1| и |a1c| - это длины векторов bb1 и a1c.
Теперь найдем длины векторов bb1 и a1c:
|bb1| = √(0^2 + 0^2 + 1^2) = √1 = 1,
|a1c| = √(1^2 + 1^2 + 0^2) = √2.
Теперь найдем скалярное произведение векторов bb1 и a1c:
bb1 • a1c = (0 * 1) + (0 * 1) + (1 * 0) = 0.
Подставим значения в формулу для cos(θ):
cos(θ) = 0 / (1 * √2) = 0.
Теперь найдем угол θ, используя арккосинус:
θ = arccos(0) = π/2 радиан или 90 градусов.
Итак, угол между прямыми bb1 и a1c равен 90 градусов.
Важно помнить, что в данном примере мы использовали конкретные значения координат точек a, b, b1, c и c1. Если координаты точек изменились, результат также будет различным.