Решить.буду признательна. основой прямой призмы является равнобедренный прямоугольный треугольник.высота призмы 10 см, а площадь боковой поверхности 40см^2.найдите радиус основы цилиндра, описанного вокруг этой призмы.
Другие вопросы по теме Геометрия
Популярные вопросы
- Tg(+45градусов)+tg(-45градусов)=2tg2 как доказать это тождество?...
3 - Что людям общаться? зачем человеку общение?...
3 - Напиши, что из членов твоей семьи тебе не нравится. действуйщие лица:...
2 - Найдите значение выражения 100^2-99^2+98^2-+2^2-1^2=...
1 - А) обозначение гласных после звука ( ц ) требует особого правила. исследуйте...
1 - Точка р -середина стороны ав, м — середина вс, к — середина ас. найдите...
1 - Необходим фонетический разбор слова лыжня для студента филологического...
3 - Решите : 3 у подобных треугольников авс и а1в1с1 а = 60о, ав = 12 см,...
1 - Cricle five mostimpotant qualities of a good journalist.write them down...
2 - Нужно . вычислите: вычислите 8 целая три четвертых умножить на два целое...
1
Цилиндр описанный, => прямоуг.треуг.вписан в окружность, => R равен половине гипотенузы
треугольник равнобедренный, по т.Пифагора
(2R)^2 = 2x^2, где x---катет
R^2 = x^2 / 2
R = x / корень(2)
Sбок.призмы = высота * (x+x+гипотенуза) = 40
2x + 2R = 40/10 = 4
x+R = 2
x = 2-R
R = (2-R) / корень(2)
2-R-Rкорень(2) = 0
2-R(1+корень(2)) = 0
R = 2 / (1+корень(2))
можно избавиться от иррациональности в знаменателе:
домножить числитель и знаменатель на сопряженное выражение (1-корень(2))
R = 2(1-V2) / ((1-V2)(1+V2)) = 2(1-V2) / (1-2) = 2(корень(2) - 1)
Дано: h=10см, S(б)=40см^2
Найти:
Делаем рисунок. Рисовать весь описаный цилиндр не обезательно, нас интересует лишь основа цилиндра.
Найдем отношение сторон друг к другу (в треугольнике ABC)
Т.к. это равнобедренный прямоугольный треугольник, то углы CAB и CBA равны 45 градусам.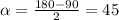
Зная угол можем сказать
Затем записываем формулу для площади боковой поверхности
AC заменяем на CB, AB заменяем на √2*CB и решаем как уравнение с неизвестной