решить :
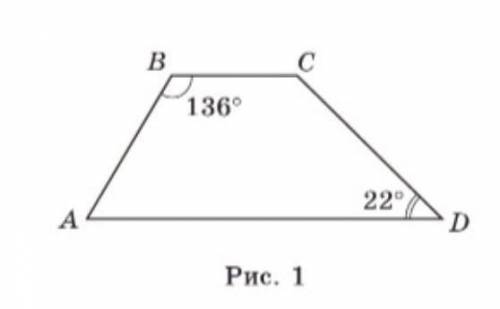
ABCD-трапеция. Кут А и С надо найти ​

Для решения данной задачи, нам необходимо использовать свойства трапеции и знания о сумме углов треугольника.

1. Свойство трапеции гласит, что основания трапеции параллельны. Изображение показывает, что отрезок AB || CD, то есть AB параллельно CD.

2. Сумма углов треугольника равна 180 градусов. Мы можем использовать это свойство, чтобы найти углы трапеции ABCD.

Для начала, давайте найдем угол А (АВС). У нас есть информация о двух углах этого треугольника: угол B (также является углом ВCD) и угол C (также является углом CDA).

Согласно свойству суммы углов треугольника, сумма углов треугольника АВС равна 180 градусов.

Угол А + угол B + угол C = 180 градусов.

Угол А + 142° + 97° = 180 градусов.

Угол А + 239° = 180 градусов.

Теперь вычтем 239° из обеих сторон уравнения.

Угол А = 180° - 239°.

Угол А = -59°.

Таким образом, угол А равен -59°.

Однако, в геометрии у нас нет отрицательных углов. Поэтому мы можем добавить 360° к углу А, чтобы найти эквивалентный положительный угол.

Угол А = -59° + 360°.

Угол А = 301°.

Теперь, чтобы найти угол С (СDA), мы можем использовать свойство, которое утверждает, что сумма углов треугольника равна 180 градусов. Таким образом, угол С равен 180° - угол C - угол A.

Угол С = 180° - 97° - 301°.

Угол С = -218°.

Однако, как и в случае с углом А, мы можем добавить 360° к углу С, чтобы найти эквивалентный положительный угол.

Угол С = -218° + 360°.

Угол С = 142°.

Таким образом, мы нашли углы А (301°) и С (142°) трапеции ABCD.